**The Nettle Magic Project** # What's All This, Then? The Nettle Magic Project is a collection of technologies intended to enable magicians (the performing kind, not the occult) to have intimate knowledge of a deck of cards during their performance: the ordered list of every card in the deck, which card(s) are missing and even which cards are face-up in the deck. A deck of cards is read by scanning card-identifying codes printed on the edges of each card. Decks can be marked with different inks, including some that are virtually invisible to the human eye (UV reactive and IR absorbing inks.) ![**LEFT**: An test deck marked on just the short sides with visible Black ink. **CENTER**: A scanning server running on a Raspberry Pi Zero W with a NoIR camera module and a 5MM IR filter. **RIGHT**: Client software running on an iPad displaying the results of a raw scan from a scanning server. The deck in this image is marked with IR absorbing ink and viewed under IR-viewing conditions.](img/intro-stages.png) A marked deck is not needed to experiment with the software. Test videos are included and in a pinch you can print your own marks on a sheet of paper for testing purposes. However, if you plan to work with a physical deck of cards you'll need an edge-marked deck. This document will describe two processes that can be used to apply edge marks to a deck of cards. The core libraries, along with the production server (_Whisper_) are written to support macOS and Linux, with additional support for the Raspberry Pi platform. The testbed applications (_Steve_ and _Abra_) were written specifically for macOS and iOS, respectively. There is currently no Windows support for desktop platforms or Android support for mobile platforms. !!! Note: Author's Note I hope you'll have fun with this and I especially hope you'll get engaged and involved. After all, I'm releasing this publicly to see ways that other creative minds can improve on this work. # Getting Up And Running The following sections will guide you through getting up and running in various hardware environments. If you have access to a Mac, I highly recommend going through the Meet Steve: The Testbed section. The testbed software provides a number of debug/diagnostic visuals which will help you get a solid understanding of how the scanning software works. 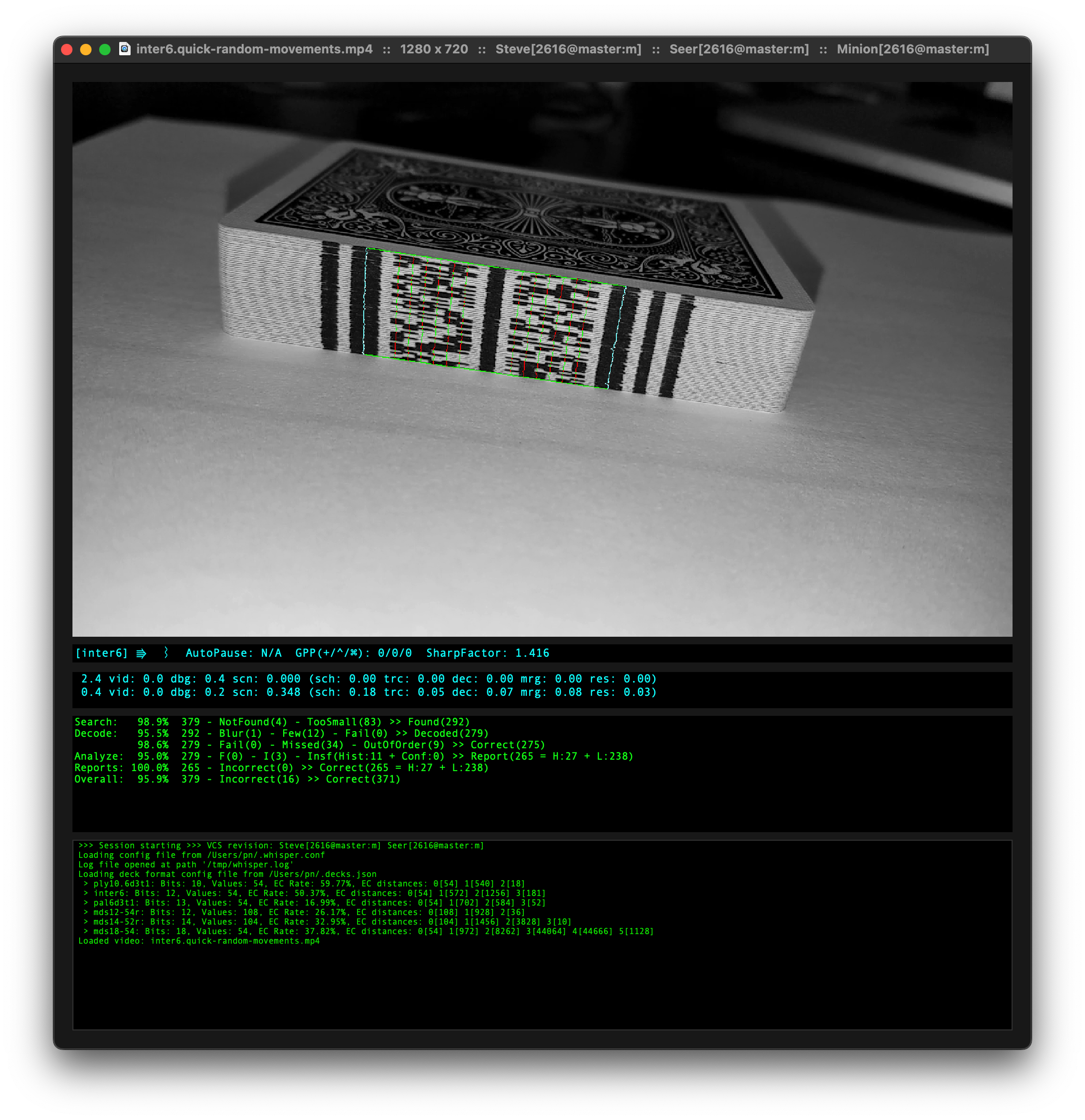## Meet Steve: The Testbed ![The testbed application running a simulation using an input video.](img/steve.png) Most of the development was done using the testbed application, named Steve. I needed a name and _Steve_ was as good a name as any. Just ask anybody named Steve. The testbed allows for easy iteration with a multitude of debugger visualizations accessible from a keypress or menu option. If you have access to a Mac, you are encouraged to explore the application with one of the supplied sample videos. Note: Steve will automatically discover the sample videos, but it also supports a drag/drop interface for your own videos or images. !!! Note: Preparing to run Steve Steve requires two configuration files. Without these files, Steve won't work very well. The first is the server/scanner configuration file, `whisper.conf`. This configuration file is loaded in cascading fashion, starting with `/etc/whisper.conf`. Next, the file `/usr/local/etc/whisper.conf` is loaded and any configuration settings in this file will override those from the previous. Finally, the file `~/.whisper.conf` is loaded, allowing user-specific configuration overrides. The second configuration file is the _Deck Definitions_ (`decks.json`). See the Deck Definitions section for details. This file is loaded in a similar cascading fashion, starting with `/etc/decks.json`. Next, the file `/usr/local/etc/decks.json` is loaded and any deck definitions in this file will override those from the previous. Finally, the file `~/.decks.json` is loaded, allowing user-specific configuration overrides. ## Meet Whisper: The Server _Whisper_ is the primary scanning server. In most production performances _Whisper_ would be deployed to a device, likely hidden on the performer or in/on a prop. The scanning results would be received from a client of some kind and incorporated into a performance. _Whisper_ is more than just a stand-alone server. It includes a text-based visual interface that can also act as a console-based testbed for development work. ![The Whisper server in console text mode running a simulation using an input video.](img/whisper.png) For supported platforms, to build whisper, simply run the 'build' script like so: ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ bash $ ./build release whisper ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ !!! Note: Preparing to run Whisper Whisper requires two configuration files. Without these files, Whisper won't work very well. The first is the server/scanner configuration file, `whisper.conf`. This configuration file is loaded in cascading fashion, starting with `/etc/whisper.conf`. Next, the file `/usr/local/etc/whisper.conf` is loaded and any configuration settings in this file will override those from the previous. Finally, the file `~/.whisper.conf` is loaded, allowing user-specific configuration overrides. The second configuration file is the _Deck Definitions_ (`decks.json`). See the Deck Definitions section for details. This file is loaded in a similar cascading fashion, starting with `/etc/decks.json`. Next, the file `/usr/local/etc/decks.json` is loaded and any deck definitions in this file will override those from the previous. Finally, the file `~/.decks.json` is loaded, allowing user-specific configuration overrides. If your build was successful and the configuration files are setup, you should be able to launch `whisper`. Uou'll find the binary in the following location: ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ base .out/release/whisper ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ As a test, you can run Whisper against one of the sample videos packaged with Steve: ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ bash .out/release/whisper -6 Sources/Steve/Steve/Reference/inter6.quick-random-movements.mp4 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ### A note about the included sample videos Many of the samples provided used an old code format called `inter6`. Decks marked with this format are recognizable as having a wide separation line down the center of the deck separating two blocks of 6-bit codes. When running simulations with videos containing decks marked with these codes, ensure that the `inter6` format is enabled in the `decks.json` file. Also, when running `whisper` be sure that you pass `-6` on the command line to select that format for scanning. 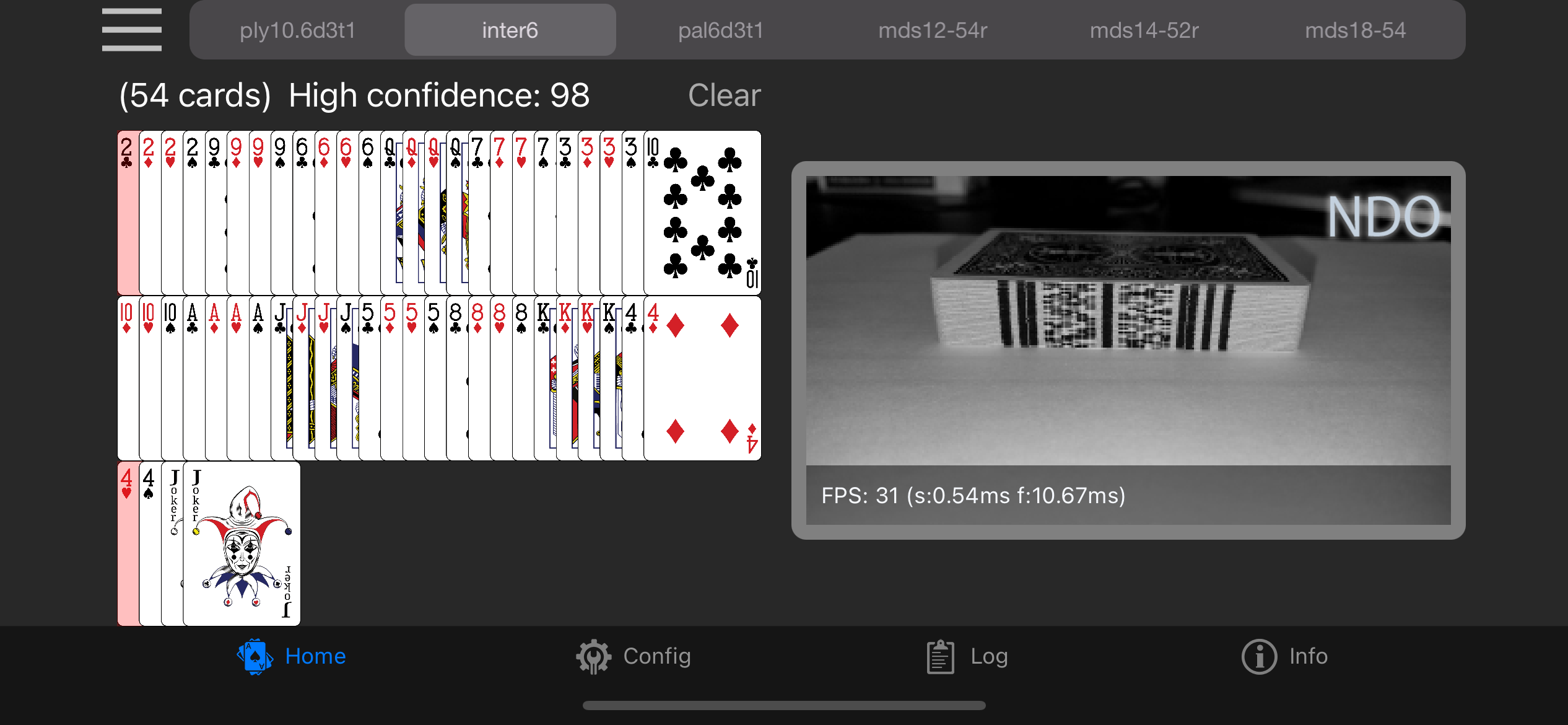## Running on an iPhone/iPad ![Abra - the iOS client application.](img/error-correction-viz.png) _Abra_ is an application that can be used to view the results of a remote scanning server. Clients/servers use a form of auto discovery to locate and communicate. Currently only one serer on a network is supported. Abra is also capable of running a local server, enabling a device to become its own scanner. Note that this requires either visible ink marks or IR marks. ## Running on a Raspberry PI During development I used cross-compilation from my Intel-based Mac to compile for Raspberry Pi. If you interrogate the `build` script, you'll see some hard-coded paths for specific toolchains I had setup. While this worked well for me, it was probably not the right way to do things. Rather than document the arcane way that I did things, perhaps other developers can tackle a better build process that includes building for (and on) a Raspberry PI. As a starting point, the code should build on a Raspberry PI, provided you have the appropriate Swift build tools installed on the device. # How It Works The diagram below provides a high-level view of the various stages of the scanning process, starting from an input frame of video and ending with a scanning result (that is, an ordered list of cards in the deck.) It's important to understand the two overarching objectives that drove virtually all decisions during development. * **Correct Results**: This may seem obvious, but let's put a finer point on it: Due to the nature of this software being intended for live performances, an incorrect result can put the performer in an awkward position. Though it's possible, it should be _very unlikely_ for scanning results to be incorrect. If there is a scanning difficulty, the result should be delayed until a confident result can be returned. * **High Performance Through Efficiency**: As you will learn in the following sections, a result is not returned from the scan of single frame of video. Rather, several frames of video are scanned and their results are analyzed and in many cases, combined. If the software is not fast enough to keep up with the video stream there is risk of losing important data that can contribute to a confident result. In addition, _Performance Through Efficiency_ results in less heat (important when the hardware may be hidden on the performer's person) and longer performance times with smaller batteries. ************************************************************************************************************************* * .------------------------. * | Input Video Frame (Luma) | * '-----------+------------' * | .------------------------. * |<-------------+ Configuration Parameters | * .------------------------. | '------------------------' * | Deck Definition +------------>| * '------------------------' | * v * .--DECK SEARCH-------------------------------------------------------------------. * | | * | .-----------------[temporal feedback]-------------------. | * | | | | * | v | | * | .--------. .---+----. | * | | Temporal | .--------------. .------------. | Temporal | | * | | Grid +--->| Landmark Trace +--->| Deck Extents +--->+ State +---. | * | | Search | '--------------' '------------' | Update | | | * | '--------' '--------' | | * | .----------------------------------------------------------------------------' | * | | .--------------------. .-----------------. | * | '-->| Deck Size Validation +--->| Gather Mark Lines | | * | '--------------------' '--------+--------' | * | | | * '-------------------------------------------|------------------------------------' * | * .-------- Mark Lines ---------' * | * .--DECODE---|--------------------------------------------------------------------. * | v | * | .-----------------. .------------------. .----------------. | * | | Readability Check +----->| Generate Bit Words +-->| Error Correction | | * | '-----------------' '-------------+----' '--------+-------' | * | ^ | | | * | | | | | * | '---|------------------' | * '-------------------------------------------|------------------------------------' * | * .------- Card Codes -------' * | * .--RESOLVE-----|-----------------------------------------------------------------. * | v | * | .-------------. .------------. .--------------------. | * | | Genocide Rule +--->| Revenge Rule +--->| History Cache Insert | | * | '-------------' '------------' '---------+----------' | * | | | * '------------------------------------------------------------|-------------------' * | * .----------- History Cache ----------' * | * .--ANALYZE------------|----------------------------------------------------------. * | v | * | .-------------------. .-----------------------------. | * | | History Cache Merge +--->| Confidence Factor Calculation | | * | '-------------------' '--------------+--------------' | * | | | * '-----------------------------------------------------|--------------------------' * .------------' * | * v * .----------------------. * | Report Result | * '----------------------' * ************************************************************************************************************************* The sections that follow will cover each stage in more detail. ## Input Configuration There are two forms of configuration information that used throughout the scanning process. The first form, the _Configuration Parameters_, are read from the **whisper.conf** file and provides global configuration for all aspects of the scanning process. From input values to various heuristics to debug visualization flags. The second form, the _Deck Definition_, provides the specification for the printed code. A Deck Definition specifies the codes printed on each card as well as the physical properties of the code. These physical properties include the physical size of the code on a printed deck and the location and spacing of the marks printed on each card. In addition, the Deck Definition provides other key information needed for decoding a marked deck. See the Deck Definitions section for more detailed information. ## Deck Search The deck search starts with a single frame of video as an 8-bit Luma (Grayscale) image. A grid of crisscrossing lines -- the _Search Grid_ -- are used to locate a line through the image that passes through the full width of the code printed on the deck. The landmarks in the printed code provide a distinctive pattern used for recognizing the deck. ************************************************************************************************************************* * Bit Columns * +-+-+-+-+-+-+-+-+-+-+-+-+ * v v v v v v v v v v v v v * ░░░██░░███░░░░█░░░░░█░░░█░░░░░░░█░░░░░█░░░░███░█░░░ * ░░░██░░███░░░░░░█░█░░░█░░░█░█░█░░░░░█░░░░░░███░█░░░ * ░░░██░░███░░░░█░░░░░░░░░█░░░░░░░█░█░░░█░░░░███░█░░░ * ░░░██░░███░░░░░░░░█░█░█░░░█░█░░░░░░░█░░░░░░███░█░░░ * ░░░██░░███░░░░█░█░░░░░░░█░░░░░█░█░█░░░░░░░░███░█░░░ * ░░░██░░███░░░░░░░░█░░░░░░░█░█░░░░░░░█░░░░░░███░█░░░ * | | | | * '--+-------------- Landmarks ----------+-' ************************************************************************************************************************* [The components of the marks on a deck. Landmarks are used to aid in locating the deck within the image. Bit Columns represent the identifying information printed on each card.] The deck's landmarks are then traced to find the top and bottom extents of the deck in the image. This full understanding of the deck's location in the frame provides the information needed to locate the columns of bits that contain the card-identifying data. These columns are scanned and the bits collected into _Mark Lines_ which can be decoded. The following sections will cover each phase of this process in more detail. ### Temporal Grid Search ![A visualization of the Search Grid configured to cover the entire frame, used to locate the deck by recognizing the pattern of landmarks printed on the deck.](img/search_grid.png) !!! Note: A Note About Visualizations In This Document Images noted as _visualizations_ in this document are rendered in real time by the testbed software, _Steve_ using various debug rendering features to show actual runtime data, results, charts, etc. Many of these debug visualizations are also available outside of the testbed software, though the ability to view them is currently somewhat limited. The _Search Grid_ is an ordered set of crisscrossing lines that cover the searchable space in the image. Starting with the first line in the Search Grid, the line is checked to see if it passes through the length of the code (that is, it passes through all of the landmarks in the code.) The process of scanning for the code from a given _Search Line_ can be thought of as an inverted line-drawing operation. Every pixel in along the line is visited, but rather than drawing the line (modifying the pixels in the image) the pixels along the line are collected into an array. Landmark detection uses a custom edge detection algorithm that is run on the array of pixels from the Search Line. If the landmark pattern matches the definition for a given deck (see the Deck Definition section) the search is halted. ![A visualization of the edge detection. The Red line indicates the Search Line being examined. The Yellow lines extending perpendicular from the Search Line (_edge markers_) indicate the direction and strength of the edge. Edge markers extend in both directions to indicate the start and end of a mark, while their length indicates the edge's relative strength. The Green lines trace the dynamic threshold. Only edge markers that cross the threshold are considered.](img/search_line_edge_detect.png) The purpose of the landmarks is to provide a distinctive pattern that can be recognized along the Search Line. If this pattern is found in the Search Line, the deck is considered found. ![A visualization showing the components of the marked deck along a Search Line (shown in Red). The position of each component from the Deck Definition (see the Deck Definitions section) is denoted with a vertical Yellow line slicing perpendicularly though the Search Line. Landmarks are represented with the addition of a Green box.](img/deck-locations.png) The relative distance between the outermost landmarks in the image can be calculated. This distance can be used to calculate a reasonable estimate of the deck's height in the image. If the height does not meet the minimum requirements for the number of pixels needed for reliable scanning, the temporal state information is updated (see the discussion below about low-fidelity updates to the Temporal State Information) and the search is aborted for this frame. If the deck was not found, the process moves on to the next Search Line in the grid until the code has been located or the entire Search Grid has been exhausted. !!! Note: Optimizing the Search Grid The number of lines in the grid, their spacing, clustering, orientation and other parameters all provide input to a heuristic that determines the grid's configuration and search-order priority. The end result is an ordered list of Search Lines that provide an efficient center-out search pattern with a high probability of finding the deck in as few searches as possible. The Search Grid includes temporal state information consisting of an offset and orientation for the grid. This information is applied to the grid at the start of the search process. This is just a fancy way of saying that the grid is moved and rotated into position where the deck was last found. The expectation is that that between frames the deck generally won't have moved very far and is often found in the next frame with the first Search Line. ![Visualizing the temporal state of the Search Grid. The starting Search Line in each image is highlighted in Red. As the images progress from A through D, the Search Grid is moved and rotated to aid in finding the deck quickly in the next frame, often with a single Search Line query.](img/temporal_grid.png) ### Landmark Trace ![Landmark traces are visualized in the blue region. The innermost landmarks are traced to find the column of pixels through the center of each landmark. This process locates the top and bottom of the deck while also providing contour information for the stacked deck.](img/contour-landmarks.png) The output of the landmark trace is a column of pixel locations through the center of each of the two innermost landmarks. As decks are rarely stacked perfectly, these columns are used to follow the contour of the stacked deck. These columns will be used later when gathering Mark Lines along the contour of the deck. !!! Note: A Note About Landmark Tracing Performance The Landmark Trace process is very CPU intensive. A standard computer vision approach might be to find the rectangular edges of the landmarks. Though this is an adequate solution, it is also very CPU intensive. The approach used here is to start at the point where the Search Line encountered the landmark and work outward from that point until the top & bottom extents of the deck are found. This is done by collecting a line segment of pixels along the Search Line's axis that covers the landmark with a small amount of overlap. This process is visualized as blue line segments in the image above. For each line segment, a rolling sum is calculated. This is similar to a rolling average but the division has been optimized out. While doing this, the smallest value - that is, the sum of the darkest pixels - is noted. This is expected to be the center of the Landmark. The process continues by stepping outward from the Search Line and repeats until the extents of the deck are reached. ### Deck Extents The deck extents are calculated from the endpoints of the center columns of the traced landmarks. From these extents the deck's exact position within the frame is known. ![A visualization of the deck extents, represented by the two Green lines connecting the endpoints of the center columns of the traced landmarks.](img/deck_extents.png) ### Temporal State Update There are two types of temporal state updates: high- and low-fidelity. A high-fidelity update uses the deck extents to calculate the center of the deck and its orientation within the image. These values are used to update the temporal state information to accurately center the Search Grid on the deck's location. A low-fidelity update is used when the search is aborted early (the deck was determined to be too small.) The deck extents haven't been calculated yet, but the Search Line used to locate the deck provides a reasonable estimate for the deck's location in the image. ### Deck Size Validation The deck extents provide the exact dimensions of the deck within the frame. These dimensions are use to precisely evaluate the size of the deck, in pixels, to ensure that it provides enough information for reliable scanning. For example, if the deck's definition (see Deck Definitions section) specifies a minimum requirement of two pixels per per card with a 52-card deck, then the deck must be at least \(2 \times 52 = 104\) pixels tall within the image to meet the minimum requirements. Scanning is aborted if the deck does not meet this requirement. ### Gather Mark Lines ![A visualization of Mark Lines used to trace through columns of bits. These Mark Lines follow the contour of the deck provided by the landmark trace process. These lines are Red where a bit is determined to be set and Green where bits are determined to be unset.](img/contour-mark-lines.png) The data bits printed on each card (_Bit Marks_) are arranged in columns when the cards are stacked into a deck. Each column of bits has a defined position relative to the innermost landmarks (see the Temporal Grid Search section.) A Mark Line refers to pixels that follow a single column for a given bit. These columns are gathered in a way similar to Search Lines, with pixels along each Mark Line being collected into an array. The landmark tracing process (see the Landmark Trace section) produces a contoured column of pixels for each of the innermost landmarks These contours provide guidance for the Mark Lines, allowing them to follow the contour of irregularly stacked decks. !!! Note: A Note About The Mark Line Approach Gathering bits along columns of Mark Lines allows for a more robust solution as this is easier than tracing the individual edges of stacked cards. In addition, this process provides for a far more efficient solution, given that it only requires reading a small fraction of the pixels in the printed code on the deck. ## Decode To understand the decoding process and how it decodes a set of Mark Lines into the internal representation of a deck of cards, it is important to first understand the input Mark Lines. As described in the previous section, each Mark Line represent the pixels extracted from the image along a column of pixels for a given data bit. If a code has 12 bits of data there will be 12 Mark Lines. The first Mark Line would be an array of pixel values representing bit 0 for all cards in the deck, followed another Mark Line for bit 1 for all cards in the deck, and so on for all 12 bits. ************************************************************************************************************************* * Mark Lines/Bit Columns * .--+---+---+---+---+---+---+---+---+---+--. * | | | | | | | | | | | | * 11 10 9 8 7 6 5 4 3 2 1 0 * | | | | | | | | | | | | * v v v v v v v v v v v v * * 1 ░ █ ░ █ █ █ █ █ █ █ █ █ * 2 ░ ░ ░ ░ ░ ░ ░ ░ █ ░ █ █ * 3 ░ ░ ░ ░ ░ ░ ░ ░ █ ░ █ █ * 4 █ █ ░ ░ █ █ ░ █ ░ ░ █ ░ * 5 █ █ █ █ █ ░ █ ░ ░ ░ ░ ░ ************************************************************************************************************************* [A visual representation of the Mark Lines for a 12-bit code, labeled across the top with the MSB on the left and the LSB on the right. Only the first 5 rows in each Mark Line are shown.] Before the decoding process begins, the column of pixels in each Mark Line is first examined for readability by performing a sharpness test. If any Mark Line is determined to be too blurry for reliable decoding, the process is aborted. Each Mark Line is then converted from an array of pixel values into an array of boolean values using a threshold. Given that each Mark Line started as a column of pixels traversing the deck within the image, it's very unlikely that the Mark Lines will each contain the same number of values. To normalize their lengths, the Mark Lines and resampled so that they each contain the same number of values, equal to or greater than the length of the longest Mark Line. The final step is to convert the arrays of bits into binary values (_Bit Words_) by combining the bits from each row in the Mark Line arrays into binary words. For a 12-bit code, each word would be a 12 bits. Error correction is applied to the resulting list of words in order to build raw set of card-identifying codes for the deck. It is important to note that the decoding process will produce more raw values than there are cards in a deck. These values will later be resolved into a proper representation of a deck (see the Resolve section.) The following sections will cover each phase of this process in more detail. ### Readability Check Readability is determined by examining the column of pixel values from each Mark Line for sharpness. If any Mark Line is determined unreadable, the scanning process is aborted. ![A visualization of sharpness. Each graph in the image represents the sharpness of a single Mark Line. The shaded area within each graph represents the minimum sharpness threshold and the Max line (shown in Red) represents the maximum value in the graph. The Max line must extend beyond the shaded region in order for the Mark Line to qualify for readability.](img/sharpness-graphs.png) Ensuring readability is important as the scan results from a low quality image source could prove untrustworthy. More importantly, these scan results could pollute the historic data used later in the analysis phase (see the Analyze section.) Readability is performed using a 4 x 1 convolution kernel on the array of pixels in each Mark Line: \begin{pmatrix} +1&+1&-1&-1 \end{pmatrix} IR imaging used with this software has proven to be an additional challenge given the low-light nature of narrow-band IR imaging. In those use cases, an IR bandpass filter and an IR LED were used that limited the incoming light to a 40nm wide window centered at 850nm in the electromagnetic spectrum. The use of sharpness verification proved quite useful in reducing unreliable results for those use cases. Note that this works especially well due to the columnar nature of the way pixels are collected for the Mark Lines. As the pixels traverse through a column of the image from the top to the bottom of the deck, the pixel-to-pixel changes tend to be high-frequency as the collection moves from card to card and from Bit Mark to Bit Mark. ### Generate Bit Words ************************************************************************************************************************* * Mark Lines/Bit Columns * .--+---+---+---+---+---+---+---+---+---+--. * | | | | | | | | | | | | * 11 10 9 8 7 6 5 4 3 2 1 0 Bit Words * | | | | | | | | | | | | .---------. * v v v v v v v v v v v v | | * * 1 ░ █ ░ █ █ █ █ █ █ █ █ █ --> 010111111111 * 2 ░ █ ░ █ █ █ █ █ █ █ █ █ --> 010111111111 * 3 ░ ░ ░ ░ ░ ░ ░ ░ █ ░ █ █ --> 000000001011 * 4 ░ ░ ░ ░ ░ ░ ░ ░ █ ░ █ █ --> 000000001011 * 5 ░ ░ ░ ░ ░ ░ ░ ░ █ ░ █ █ --> 000000001011 * 6 ░ ░ ░ ░ ░ ░ ░ ░ █ ░ █ █ --> 000000001011 * 7 ░ ░ ░ ░ ░ ░ ░ ░ █ ░ █ █ --> 000000001011 * 8 ░ ░ ░ ░ ░ ░ ░ ░ █ ░ █ █ --> 000000001011 * 9 █ █ ░ ░ █ ░ ░ ░ █ ░ █ █ --> 110010001011 * 10 █ █ ░ ░ █ █ ░ █ ░ ░ █ ░ --> 110011010010 * 11 █ █ ░ ░ █ █ ░ █ ░ ░ █ ░ --> 110011010010 * 12 █ █ ░ ░ █ █ ░ █ ░ ░ █ ░ --> 110011010010 * 13 █ █ ░ ░ █ █ ░ █ ░ ░ █ ░ --> 110011010010 * 14 █ █ ░ ░ █ █ ░ █ ░ ░ █ ░ --> 110011010010 * 15 █ █ █ █ █ █ ░ █ ░ ░ █ ░ --> 111111010010 * 16 █ █ █ █ █ ░ █ ░ ░ ░ ░ ░ --> 111110100000 * 17 █ █ █ █ █ ░ █ ░ ░ ░ ░ ░ --> 111110100000 * 18 █ █ █ █ █ ░ █ ░ ░ ░ ░ ░ --> 111110100000 * 19 █ █ █ █ █ ░ █ ░ ░ ░ ░ ░ --> 111110100000 * 20 █ █ █ █ █ ░ █ ░ ░ ░ ░ ░ --> 111110100000 ************************************************************************************************************************* [A visual representation of the Mark Lines for a 12-bit code, labeled across the top with the MSB on the left and the LSB on the right. Only the first 20 bits in each Mark Line are shown. The binary values along the right can be thought of as a table rotation, in which the bits for a given row in each Mark Line are combined into a single binary word.] In order to decode the Mark Lines into codes marked on the edges of each card, the Mark lines must first be binarized. Each Mark Line is converted from an array of pixel values into an array of boolean values called _Bit Columns_. This binarization process involves a threshold that is calculated from the min/max range of all pixel values in a given Mark Line and then applied to each pixel to determine its associated boolean value. It is important to note at this point that it is very unlikely that the full set of Bit Columns will all be the same length. In practice, decks in the image are rarely perfectly perpendicular to the camera. Any amount of perspective or rotation (or likely both) will causes one side of the deck to be larger in frame than the other. The length of the Bit Columns will reflect this. To normalize their lengths, each Bit Column is resampled to a normal length. The normal length is calculated using a _Resample Factor_ multiplied by the number of cards in the deck's definition. With a common Resample Factor of 5 and a deck of 52 cards, each Bit Column would result in an array of 260 boolean values. The final step is to convert the Bit Columns into binary values (_Bit Words_) by combining the bits from each row in the set of Bit Column arrays into binary words. For a 12-bit code, each Bit Word would be a 12 bits. !!! Note: A Note About The Resample Factor The Resample Factor plays an important role in the decoding process. Given the nature of the Bit Columns being different lengths, its likely that some cross-talk between rows of bits will take place when converting rows of Bit Columns into Bit Words. By _stretching out_ this data, Card Codes may show up in the data where they otherwise might not have. ### Error Correction Error correction is applied to the resulting list of Bit Words in order to build raw set of card-identifying codes for the deck. Codes that are error corrected are noted as such. This information helps determine the confidence factor. In addition, cards that required error correction can be displayed in the companion app (Abra) which can be useful during the marking process to discover cards that are difficult to read. It is important to note that the decoding process will produce more raw codes than there are cards in a deck. Note the previous example of the Bit Columns being normalized to 260 values. In that case, the this process will generate 260 Bit Words. These Bit Words represent our initial set of _Card Codes_ (that is, card-identifying codes printed on the edges of each card.) These Card Codes are resolved into a proper representation of a deck in the next section (see the Resolve section.) For more information on the error correction employed, see the Error Correction Codes section. ## Resolve The Resolve process begins with a diffuse set of _Card Codes_ that contains many duplicate entries, invalid entries (codes that do not match a Card Code) and incorrect (out of order) entries. This set must be resolved to an ordered list of cards in the deck. Resolving this diffuse set of Card Codes into a proper ordered list of Card Codes that represent the deck is a two-step process that makes use of pair of logical set reductions: * Genocide Rule - Assigns weights to clusters of Card Codes, then removes all but the largest cluster for each Card Code. * Revenge Rule - Collapses clusters of Card Codes into a single Card Code. The resulting ordered list of Card Codes represents the final _Deck_. This Deck is added to a _History Cache_ which stores recently decoded decks. This History Cache plays a crucial role in the Analysis phase (see the Analysis section). The following sections will cover each phase of this process in more detail. ### Genocide Rule ************************************************************************************************************************* * Code Initial After Genocide * .---------. .-----------------. .-----------------. * | | | | | | * * 010111111111 --> Ace ♣ --> Ace ♣ * 010111111111 --> Ace ♣ (weight = 2) --> Ace ♣ (weight = 2) * 000000001011 --> Two ♣ --> Two ♣ * 000000001011 --> Two ♣ --> Two ♣ * 000000001011 --> Two ♣ --> Two ♣ * 000000001011 --> Two ♣ --> Two ♣ * 000000001011 --> Two ♣ --> Two ♣ * 000000001011 --> Two ♣ (weight = 6) --> Two ♣ (weight = 6) * 110010001011 --> ? --> ? * 110011010010 --> Four ♦︎ --> Four ♦︎ * 110011010010 --> Four ♦︎ --> Four ♦︎ * 110011010010 --> Four ♦︎ --> Four ♦︎ * 110011010010 --> Four ♦︎ --> Four ♦︎ * 110011010010 --> Four ♦︎(weight = 5) --> Four ♦︎(weight = 5) * 111111010010 --> Six ♥︎ * 111111010010 --> Six ♥︎(weight = 2) * 111110100000 --> Jack ♥︎ --> Jack ♥︎ * 111110100000 --> Jack ♥︎ --> Jack ♥︎ * 111110100000 --> Jack ♥︎ --> Jack ♥︎ * 111110100000 --> Jack ♥︎ --> Jack ♥︎ * 111110100000 --> Jack ♥︎(weight = 5) --> Jack ♥︎(weight = 5) * 111111010010 --> Six ♥︎ --> Six ♥︎ * 111111010010 --> Six ♥︎ --> Six ♥︎ * 111111010010 --> Six ♥︎ --> Six ♥︎ * 111111010010 --> Six ♥︎ --> Six ♥︎ * 111111010010 --> Six ♥︎(weight = 5) --> Six ♥︎(weight = 5) ************************************************************************************************************************* [A partial visualization of a diffuse set of Card Codes along with their associated playing card representation. Each cluster of cards is given a weight, shown next to the last Card Code in each cluster. Note the two clusters of the Six of Hearts in the Initial column and that the cluster is not present in the After Genocide column.] The _Genocide Rule_ is a logic rule for eliminating statistically incorrect codes from a diffuse list. It gets its namesake from the way in which it judiciously eliminates clusters of like Card Codes. The Genocide Rule is stated as follows: > "The Genocide Rule is intended to seek out any occurrences of errant card clusters (i.e., more than > one instance of a card cluster in the entire set.) The two card clusters are challenged and if a winner is > chosen, the losing cluster is removed from the deck." The _challenge_ referred to in the quote above refers to a heuristic that is run against the competing card clusters. In the example above notice the two clusters of the Six of Hearts. The first cluster has a weight of 2 (only two consecutive occurrences of the card) while the second cluster has a weight of 5. Assuming the heuristic for the Genocide Rule chooses the second (larger) cluster as the winner, then the losing (first) cluster is removed from the list. If there were more clusters scattered throughout the set of Card Codes, then those would also be added to the challenge. Note that it is possible that the challenge may not pick a winner. In this case the cluster remains duplicated. The Analyze phase (see the Analyze section) can often resolve these conflicts. ### Revenge Rule ************************************************************************************************************************* * Initial After Genocide After Revenge * .-----------------. .-----------------. .-----------------. * | | | | | | * * Ace ♣ --> Ace ♣ * Ace ♣ (weight = 2) --> Ace ♣ (weight = 2) --> Ace ♣ (weight = 2) * Two ♣ --> Two ♣ * Two ♣ --> Two ♣ * Two ♣ --> Two ♣ * Two ♣ --> Two ♣ * Two ♣ --> Two ♣ * Two ♣ (weight = 6) --> Two ♣ (weight = 6) --> Two ♣ (weight = 6) * ? --> ? * Four ♦︎ --> Four ♦︎ * Four ♦︎ --> Four ♦︎ * Four ♦︎ --> Four ♦︎ * Four ♦︎ --> Four ♦︎ * Four ♦︎(weight = 5) --> Four ♦︎(weight = 5) --> Four ♦︎(weight = 5) * Six ♥︎ * Six ♥︎(weight = 2) * Jack ♥︎ --> Jack ♥︎ * Jack ♥︎ --> Jack ♥︎ * Jack ♥︎ --> Jack ♥︎ * Jack ♥︎ --> Jack ♥︎ * Jack ♥︎(weight = 5) --> Jack ♥︎(weight = 5) --> Jack ♥︎(weight = 5) * Six ♥︎ --> Six ♥︎ * Six ♥︎ --> Six ♥︎ * Six ♥︎ --> Six ♥︎ * Six ♥︎ --> Six ♥︎ * Six ♥︎(weight = 5) --> Six ♥︎(weight = 5) --> Six ♥︎(weight = 5) ************************************************************************************************************************* [A partial visualization of a process of diffuse set reduction starting with the Initial set and passing through the Genocide and Revenge rules. Notice compaction of the clusters into weighted Cards in the After Revenge column.] The _Revenge Rule_ is a logic rule for reducing clusters of neighboring codes from a diffuse list. It gets its namesake from the way in which it follows the Genocide rule and eliminates all but a single weighted card from each cluster. The Revenge Rule is stated as follows: > "The Revenge rule is intended to locate all duplicates and remove the neighbors. It is possible for duplicates to remain > in the set following a revenge." !!! Note: A Note From The Author About The Revenge Rule In early development the Revenge Rule was far more complex than what it is today (little more than simple set reduction of consecutive codes.) But the name was catchy and so it stuck. Note that unresolved conflicts -- duplicate entries -- from the Genocide Rule will remain present, though reduced to a single entry, after the Revenge Rule has processed the set. It is expected that the the Analyze phase (see the Analyze section) can often resolve these conflicts. The final set of Cards Codes is collected into a simple array and inserted into the History Cache. ### History Cache Insert The _History Cache_ stores the recent history of scan results (ordered set of Card Codes.) One cache entry contains two key pieces of information: 1. A unique set of ordered Card Codes (the output from the Revenge Rule) 2. An array of timestamps that represent when that particular ordered set was inserted Upon inserting an ordered set of Card Codes into the History Cache, the cache is first searched to see if a duplicate set already exists. If so, the current timestamp is added to the existing cache entry. Otherwise, a new cache entry is added with the current timestamp. In addition to this, each time a cache entry is added the cache is pruned of all expired entries. !!! Note: A Note About The History Cache Lifetime The lifetime of entries in the History Cache is generally quite short, on the order of only a few seconds. It is important that the cache lifetime is shorter than the time it would take to modify the deck and rescan it. The reason for this will be made clear in the following Analyze section, but the short of it is that the entries in the History Cache are merged into a single, confident result. If the History Cache expiration were too long, there is risk that the deck could be modified (for example, a card removed) and that resulting deck's scan competing with old cache entries which did not contain the missing card. In this case, it's quite possible that the Analysis phase could re-insert the missing card based on old cache entries. The resulting History Cache is then sent to the Analyze phase for statistical analysis. ## Analyze Scanning binary codes from the edges of cards that are ~0.3MM thick, under the low-light conditions of narrow-band IR imaging, worn or aged cards, and decks held in the hand of a performer, can present quite a challenge to the scanning process. Even under these conditions the scanning results are _generally_ reliable but they are not _always_ reliable. The goal of the Analyze phase is to combine the results from scans that are _mostly_ correct with scans that _may actually be_ correct to produce a single, confident result. The Analyze process begins by merging the scan results from all recent entries in the History Cache into a single _super result_. This process can correct errant errors in some results based on statistical analysis across the entire History Cache. From this process, a single scan result is produced. A confidence factor is then calculated and the result is released (see the Result section.) The following sections will cover each phase of this process in more detail. ### History Cache Merge The _History Cache Merge_ process uses the information from all entries in the _History Cache_ to generate a single, confident result. Consider a simplified ordered set containing only 10 values, each alphabetically labeled from A to J. This ordered set could be linked in the following way (using ○ to represent the head of the list and ● to represent the tail): ************************************************************************************************************************* * ○ -> A -> B -> C -> D -> E -> F -> G -> H -> I -> J -> ● ************************************************************************************************************************* Next, consider the following set of linked results: ************************************************************************************************************************* * Entry #1: ○ -> A -> B -> C -> D -> E -> F -> G -> H -> I -> J -> ● * Entry #2: ○ -> A -> B -> C -> D -> E -> F -> G -> H -> I -> J -> ● * Entry #3: ○ -> A -> B -> C -> D -> F -> G -> H -> I -> J -> ● * Entry #4: ○ -> A -> B -> C -> D -> E -> F -> G -> H -> I -> J -> ● * Entry #5: ○ -> A -> B -> C -> D -> E -> F -> G -> H -> I -> J -> ● ************************************************************************************************************************* To the casual observer it appears that the missing _E_ from Entry #3 was simply missed during the scanning process. The incorrect entry could be discarded. However, this would reduce the overall confidence of the final result because Entry #3 agrees with the other results that, for example, I follows H in the links. As an alternative, given enough evidence provided by the other entries, Entry #3 could be patched to include the missing link to _E_. After all, all of the other entries agree that _E_ falls between _D_ and _F_. This alternative allows us to maintain a higher level of confidence in the final result. This simple example can be extended to far more complex scenarios. Consider a History Cache of 32 entries, all of which disagree not only on the presence of values in each scan but their order as well. When presented with this scenario, it can be difficult for even the experienced observer to discern the correct result. For complex scenarios like this, a different way to represent the data is needed. *********************** * ○ -> B:8, A:24 * * A -> B:24 * * B -> C:26, H:1, D:2 * * C -> D:30 * * D -> E:28, F:2 * * E -> F:29 * * F -> G:32 * * G -> H:31 * * H -> I:32 * * I -> J:31, C:1 * * J -> ●:29, C:2, E:1 * *********************** Take a moment to study the example above. Each line in this table represents the linkages for a single entry. The first line can be read as "_The head links to B in 8 results and links to A in 24 results._" The next line could be read as "_A links to B in 24 results_." These _Link Counts_ play an important role not only in the History Cache Merge phase, but also in the _Confidence Factor_ calculation (see the Confidence Factor Calculation section.) In the example above, it's clear that there is some confusion as to what the correct result should be. The goal of the History Cache Merge process is to resolve as many of these ambiguities as possible. All results agree that _F_ links to _G_, but they disagree on what value links to _F_ (is it _D_ or _E_?) Looking closer, it seems obvious that the correct answer is that _E_ links to _F_ given that this was the case in 29 of the results, while only two results found that _D_ linked to _F_. Given the evidence, the links between _D_ and _F_ should be removed. In addition, the removed Link Count should then be attributed to the correct link between _E_ and _F_, increasing that value by 2 (from 29 to 31.) The same logic can be applied to many of the other entries. Here's the same example with the errors removed and the Link Counts adjusted accordingly: ************* * ○ -> A:32 * * A -> B:24 * * B -> C:30 * * C -> D:32 * * D -> E:28 * * E -> F:31 * * F -> G:32 * * G -> H:32 * * H -> I:32 * * I -> J:31 * * J -> ●:29 * ************* This small amount of patching was able to produce the correct result from a non-trivial case. There is an additional pass that interrogates the set for missing cards and if a missing card appears anywhere in the history, it is attempted to be inserted into the result set at the appropriate location. This is especially important for top or bottom cards in the deck as they sometimes tend to flare away from the rest of the stack and avoid detection. There are scenarios where the process simply cannot converge on a single merged history with confidence. In these cases, the Analysis is aborted and a result of _Inconclusive_ is returned. !!! Note: A Note About Very Complex Scenarios Not presented in this text are even more complex scenarios, such as cyclic ambiguities. In these scenarios, a patch in one result can open the door to allow other, previously unavailable patches to take place. ### Confidence Factor Calculation The _Confidence Factor_ for a result provides a simple percentage on a linear scale that represents the likelihood of any particular result being correct. The global _Configuration Parameters_ for the system (see the Input Configuration section) provides a threshold for high confidence results. Any result that meets or exceeds this threshold is considered a high confidence result. In addition, there is a Configuration Parameter to enable low confidence results. If low confidence reports are not enabled or the result does not meet the minimum confidence threshold, the scanning process is aborted. The calculation of a Confidence Factor is simple and straight forward. In the History Cache Merge section, the concept of _Link Counts_ was introduced. These Link Counts play an important role in the confidence factor calculation. Let's review the final example from that section: ************* * ○ -> A:32 * * A -> B:24 * * B -> C:30 * * C -> D:32 * * D -> E:28 * * E -> F:31 * * F -> G:32 * * G -> H:32 * * H -> I:32 * * I -> J:31 * * J -> ●:29 * ************* The _Confidence Calculation_ is simply the average of all Link Counts taken as a percentage of the total number of entries in the History Cache. For the example above, this average would be **30.27** \begin{equation} \frac{32 + 24 + 30 + 32 + 28 + 31 + 32 + 32 + 32 + 31 + 29}{11} = 30.27 \end{equation} As a reminder, the total number of History Cache entries from this example was 32. Therefore, the Confidence Factor for this result would be: \begin{equation} \frac{30.27}{32} \times 100 = 94.59% \end{equation} ## Report Result At the end of the scanning process a result is generated that will take one of the following forms: > **Failed** > > The scan failed, either due to a failed search or failed decode. > In addition, the result may include either a search or a decoding failure. > > A failed search could take the form of: > - _Not Found_: The deck was not found in frame > - _Too Small_: The deck was determined to be too small in frame for reliable scanning > > A failed decode could take the form of: > - _Not Sharp_: Scanning was aborted because the Readability Check failed (see the Readability Check section.) > - _Too Few Cards_: Scanning was aborted because the decoded set of cards did not meet the minimum requirement > - _General Failure_: This is the catch-all for other decoding failures > > **Inconclusive** > > A deck was scanned but the analysis determined that the result was > inconclusive. In this case, a deck is returned but the client should > not present this as a valid result. > > **Insufficient History** > > A deck was scanned but there wasn't enough history to determine confidence. > In this case, a deck is returned but the client should not present this as > a valid result. > > **Insufficient Confidence** > > A deck was scanned but the Confidence Factor was below the minimum > requirement. In this case, a deck is returned but the client should not > present this as a valid result. The Confidence Factor is also included > in the result. > > **Success (low confidence)** > > A deck was scanned and meets the minimum Confidence Factor requirement. > In this case, if low confidence results are enabled, a deck is returned > along with the Confidence Factor. > > **Success (high confidence)** > > A deck was scanned and meets or exceeds the high Confidence Factor. In > this case, a deck is returned along with the Confidence Factor. The final result is reported via the server interface to all connected clients. ![The _Abra_ client displaying the results from a scan.](img/error-correction-viz.png) # Deck Definitions _Deck Definitions_ are loaded from the **decks.json** file and provide the specifications for each printed code. The following sections provide more detail on the Deck Definition and its uses. ## The Fields of a Deck Definition The following JSON fields are used to define a Deck Definition in its entirety: (###) **id** integer A unique identifier assigned to this Deck Definition. This value is sent along with a result to each connected client, which may key off of the ID for specific functionality. This should be a 32-bit unsigned integer. (###) **ignored** Boolean, default = false If true, this format is ignored for runtime use. This value has no effect for off-line tools, such as CardBars, which work on Deck Definitions. (###) **name** String The official name for the Deck Definition. (###) **description** String The description for the Deck Definition. (###) **type** String One of: * **normal**: A standard, mono-directional code * **palindrome**: A bi-directional code that reads the same in both directions * **reversible**: A bi-directional code that reads differently in each direction For more information, see the Reversible & Palindrome Codes section. (###) **invertLuma** Boolean, default = false If true, the deck uses inverted luma. This should only be used for decks marked with inks that fluoresce (such as UV reactive inks) and not for inks that absorb light (such as visible inks or IR absorbing inks.) (###) **physicalLengthMM** Floating point The length of the longest edge of a card, in millimeters. (###) **physicalWidthMM** Floating point The length of the shortest edge of a card, in millimeters. (###) **printableMaxWidthMM** Floating point The maximum width of the printed code. If a code is intended to be printed on all sides of a deck, this value should represent the widest code that will fit on all four sides. Note that this should take into account that codes cannot be marked all the way to the ends of a card given that most cards have rounded edges. This value is used by the off-line tool CardBars to verify the marks do not exceed the maximum printable region of the card. (###) **physicalStackHeight52CardsMM** Floating point The physical height (in millimeters) for a full stack of 52 cards. If the Deck Definition includes more or fewer cards, it uses this value to calculate the stack height based on the number of cards in the definition. (###) **physicalCompressedStackHeight52CardsMM** Floating point The physical height (in millimeters) for a full stack of 52 cards that have been compressed. Similar to _physicalStackHeight52CardsMM_, this value represents the height of the stack under compression. This value was originally intended for marking tools that marked the full stack at once (such as from a modified printer) where the stack is held in place in a holder that compresses the deck tightly together. (###) **minCardCount** Integer The minimum number of cards required for decoding a deck. If the number of cards does not meet this minimum value, the deck will fail to decode with the designation _Too Few Cards_ (see the Report Result section.) Note that this value also used to determine the minimum height of a deck in the image being scanned. (###) **cardCodesNdo** Array of integers An array of integer values that represent the codes printed on the edges of cards. The order of the codes in this array defines the deck's New Deck Order (NDO.) This array is usually output from _mdscodes_. See the Generating Codes with mdscodes section for more information on generating these codes. This array must contain at least as many codes as **faceCodesNdo**. Any additional Card Codes will be ignored. (###) **faceCodesNdo** Array of strings The _Face Codes_ for each card in the deck, in New Deck Order (NDO.) The length of this array must match the length of **faceCodesTestDeckOrder**. Face Codes can take whatever form the client wishes. Current clients have adopted the standard of following two-character Face Codes for decks of standard Poker decks: ************************************ * Value Suit * *------------ --------------- * * A - Ace H - Hearts * * 2 - Two C - Clubs * * 3 - Three D - Diamonds * * 4 - Four S - Spades * * 5 - Five * * 6 - Six * * 7 - Seven * * 8 - Eight * * 9 - Nine * * T - Ten * * J - Jack * * Q - Queen * * K - King * ************************************ [The components of the two-character codes for poker decks. They are combined such as **AS** (Ace of Spades), **7D** (Seven of Diamonds), **TH** (Ten of Hearts), etc.] In addition to the standard 52 cards, Poker decks are often packaged with two Jokers and two ad cards. These can be included using the following Face Codes: * **X1** (Black & White Guarantee Joker) * **X2** (Color Joker) * **Z1** (2-sided Ad Card) * **Z2** (1-sided Ad Card) (###) **faceCodesTestDeckOrder** Array of strings The _Face Codes_ for each card in the deck, in Test Deck Order. The length of this array must match the length of the codes in **faceCodesNdo**. This is intended for testing to allow the software to recognize correct scanning results from test videos. If the deck in a test video is in New Deck Order (NDO) then this array should mirror **faceCodesNdo**. (###) **marks** Array of Mark Definitions _Mark Definitions_ define how each card is marked, including the Landmark placement, Bit Mark placement, and Spaces. Each _Mark Definition_ is an object consisting of: - **widthMM** (Floating point) - The width of the printed mark (or non-printed space.) - **type** (String) - The type of the mark, which must be one of: - _Landmark_: A portion of the code marked on all cards. - _Space_: A non-printed space. - _Bit_: A Bit Mark printed on the edge of the card, unique per card. It is important that the number of _Bit_ marks match the number of bits in the codes listed in **cardCodesNdo**. ## Deck Definitions Requirements and Guidelines Creating a valid Deck Definition requires care. It is recommended to start with an existing Deck Definition and only modify as needed. If a new Deck Definition must be created from scratch, the following guidelines may be helpful: A code's physical printed width is the sum of all **widthMM** values of all Mark Definitions. This sum must be less than or equal to **printableMaxWidthMM**. Each _Bit_ in the **marks** array represents a bit position in the codes printed on the edge of a card. If the **cardCodesNdo** defines an array of 14-bit values, then there must be exactly 14 _Bit Marks_ in the Deck Definition. It is strongly recommended that innermost landmarks are the widest. This allows the landmark tracing process (see the Landmark Trace section) the ability to follow the contours of the deck's stack. A rule of thumb is that the deck's irregular stacking can deviate only as much as half of the inner landmark width. Deck Definitions that are **reversible** or **palindrome** must use **marks** in the Deck Definition that are also reversible. That is, the landmarks, spaces and bits are arranged such that the printed code is palindromic. This allows marks on cards that are face-up in the deck to line up with their inverted neighbors. **Reversible** and **Palindrome** codes also require that the printed marks be perfectly centered on the deck. Codes that do not meet this requirement will be skipped with an error in the logs. Similarly, Deck Definitions that are **normal** (and not **reversible** or **palindrome**) must not use **marks** that are palindromic as this can prevent the deck from being scanned in the correct orientation. If either of these two requirements is not met, an error will be logged and the Deck Definition will be ignored. The software includes various validations on Deck Definitions to ensure best use. Watch for hints or warnings in the log output from CardBars. ## An Example Deck Definition ~~~~~ { "id": 23, "ignored": false, "invertLuma": false, "type": "normal", "name": "ply10.6d3t1", "description": "Polynomial Matrix 10,6 / d=3 / t=1", "physicalLengthMM": 88.2, "physicalWidthMM": 63.0, "printableMaxWidthMM": 55.0, "physicalStackHeight52CardsMM": 15.6, "physicalCompressedStackHeight52CardsMM": 15.07037037037037, "minCardCount": 35, "cardCodesNdo": [ 67, 547, 326, 907, 219, 534, 319, 874, 151, 623, 402, 806, 238, 863, 478, 706, 423, 654, 80, 759, 58, 920, 118, 1010, 300, 958, 352, 636, 266, 560, 132, 602, 200, 821, 162, 844, 461, 768, 436, 585, 504, 740, 385, 680, 101, 889, 28, 941, 177, 980, 281, 787, 341, 669, 491, 517, 41, 699, 253, 993, 15, 721, 371, 967 ], "faceCodesNdo": [ "AH", "2H", "3H", "4H", "5H", "6H", "7H", "8H", "9H", "TH", "JH", "QH", "KH", "AC", "2C", "3C", "4C", "5C", "6C", "7C", "8C", "9C", "TC", "JC", "QC", "KC", "KD", "QD", "JD", "TD", "9D", "8D", "7D", "6D", "5D", "4D", "3D", "2D", "AD", "KS", "QS", "JS", "TS", "9S", "8S", "7S", "6S", "5S", "4S", "3S", "2S", "AS", "X1", "X2" ], "faceCodesTestDeckOrder": [ "AH", "2H", "3H", "4H", "5H", "6H", "7H", "8H", "9H", "TH", "JH", "QH", "KH", "AC", "2C", "3C", "4C", "5C", "6C", "7C", "8C", "9C", "TC", "JC", "QC", "KC", "KD", "QD", "JD", "TD", "9D", "8D", "7D", "6D", "5D", "4D", "3D", "2D", "AD", "KS", "QS", "JS", "TS", "9S", "8S", "7S", "6S", "5S", "4S", "3S", "2S", "AS", "X1", "X2" ], "marks": [ {"widthMM": 3.0, "type": "Landmark"}, {"widthMM": 1.5, "type": "Space"}, {"widthMM": 2.0, "type": "Landmark"}, {"widthMM": 1.5, "type": "Space"}, {"widthMM": 4.0, "type": "Landmark"}, {"widthMM": 1.5, "type": "Space"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 2.0, "type": "Bit"}, {"widthMM": 1.5, "type": "Space"}, {"widthMM": 4.0, "type": "Landmark"}, {"widthMM": 1.5, "type": "Space"}, {"widthMM": 2.0, "type": "Landmark"} ] } ~~~~~ # Error Correction Codes The error correction described in this section is based on a traditional method but deviates in various ways. The following sections will provide more detail on this implementation and how it differs from the traditional method. Note that in the following sections, the general term _error correction_ will be used to refer to this specific implementation. ## A Quick Primer On Error Correction For those not familiar with error correction, this primer will attempt to ease the reader into these concepts, breaking through the barrier to entry one brick at a time. This error correction relies heavily on recognizing differences in strings of ones and zeros. Clever readers may recognize a similarity to _binary values_. Be warned, clever reader, that the binary values presented throughout this section should only be interpreted as strings of ones and zeros and nothing more. Their integer value (as decimal, hexadecimal, etc.) is entirely inconsequential. ********************************************************** *0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 * *0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 * * ● ● ● ● ● ● ● * *─────────────── ─────────────── ─────────────── * * diff = 1 diff = 6 diff = 0 * * * * * *0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 0 * *1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 * *● ● ● ● ● ● ● ● ● ● ● ● * *─────────────── ─────────────── ─────────────── * * diff = 8 diff = 0 diff = 4 * * * * * *1 1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 * *1 1 1 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 * * ● ● ● ● ● ● ● ● ● ● * *─────────────── ─────────────── ─────────────── * * diff = 2 diff = 8 diff = 0 * ********************************************************** [Examples of differences between pairs of 8-bit binary values. A dot appears in the line below each pair to identify differing bits. The total number of differences is noted below each pair.] The number of bits that differ in a pair of binary values is called the _Hamming Distance_. A Hamming Distance of **0** indicates the binary values are identical, with larger Hamming Distances indicating greater _differences_ between them. Though the formal term is _Hamming Distance_, it would not have been inaccurate if the term _Hamming Difference_ had been used. Hamming Distances play a key role in error correction because the more _distant_ two values are from each other, the easier it is to detect errors. Consider a contrived example in which a switch transmits its On/Off state over an unreliable network. Rather than transmitting a single bit for each state, the designers decided to use 8-bit _codes_. They assigned the code **00000000** for the Off state and the code **11111111** for the On state. These codes allow an external receiving device to perform some amount of error correction. If the value **00010000** was received, it seems fairly probable -- perhaps even intuitive -- that the value received had a single corrupt bit and should instead be **00000000**. This intuition can be codified using Hamming Distances: ************************************** * Off State Code On State Code * * * *0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 * *0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 * * ● ● ● ● ● ● ● ● * *─────────────── ─────────────── * * Distance = 1 Distance = 7 * ************************************** [Using the Hamming Distance to show that a corrupted value (**00010000**) is closer (that is, it has a smaller Hamming Distance) to the Off state than to the On state.] Not all errors can be corrected. The number of errors that can be corrected can be calculated using the formula: \begin{equation} \Big\lfloor \frac{(d - 1)}{2} \Big\rfloor \end{equation} In the above formula, substitute \(d\) with the minimum distance between codes. Given that the Hamming Distance between the On/Off codes is _8_, the formula states that this set of codes provides error correction with up to _3_ errors: \begin{equation} \Big\lfloor \frac{(8 - 1)}{2} \Big\rfloor = 3 \end{equation} !!! Note: An Important Note About The Error Correction Limit If a set of codes does not have a minimum distance of at least 3, the codes cannot be error corrected. Consider what would happen if a value with 4 errors (**01010011**) had been received: ************************************** * Off State On State * * * *0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 * *0 1 0 1 0 0 1 1 0 1 0 1 0 0 1 1 * * ● ● ● ● ● ● ● ● * *─────────────── ─────────────── * * Distance = 4 Distance = 4 * ************************************** [A case in which the Hamming Distance of a severely corrupted value (**01010011**) is equally distant to each On/Off state code. In this case, the error correction is deemed inconclusive.] !!! Note: A Note About Correctness This error correction makes no attempt at proving correctness. It is possible for a value to be so corrupt as to be mistaken for another code or even error-corrected to the wrong code. It is up to the overarching system to determine correctness (for example, by use of a checksum or hash on the final set of error corrected data.) The example above uses the codes **00000000** and **11111111** because of the large Hamming Distance between them. Any pair of codes with an equal distance would work just as well. For example, consider replacing the original Off state code with **10101100** and the On state code with **01010011**. This new pair of codes has the same Hamming Distance (**8**) as the original pair, making them just as error-correctable. A received Off state code with a single error (**10111100**) would produce the same result: ************************************** * Off State On State * * * *1 0 1 0 1 1 0 0 0 1 0 1 0 0 1 1 * *1 0 1 1 1 1 0 0 1 0 1 1 1 1 0 0 * * ● ● ● ● ● ● ● ● * *─────────────── ─────────────── * * Distance = 1 Distance = 7 * ************************************** This contrived example was intended to highlight the importance of maximizing the distance between codes in order to maximize the ability to correct errors. Most applications will need to work with data more complex than On/Off states. Let's expand the contrived example to support a variable switch with 8 positions while reducing the size of each code to 6 bits. Consider the following set of codes: ********************** * Code Position * *-------- --------- * * 101101 1 * * 011011 2 * * 011100 3 * * 000111 4 * * 101010 5 * * 110001 6 * * 110110 7 * * 000000 8 * ********************** The set of codes above provides one code for each of the 8 switch positions while still providing error correction. As stated previously, the number of errors that can be corrected is determined by the distance between pairs codes in the set. The following table shows the distances from each possible pair of codes in the set: ***************************************************************************************** * | * |101101 011011 011100 000111 101010 110001 110110 000000 *-------+-------------------------------------------------------- * 101101| 3 3 4 3 4 4 3 * 011011| 3 4 3 4 3 3 4 * 011100| 3 4 3 4 3 3 4 * 000111| 4 3 3 3 4 4 3 * 101010| 3 4 4 3 3 3 4 * 110001| 4 3 3 4 3 4 3 * 110110| 4 3 3 4 3 4 3 * 000000| 3 4 4 3 4 3 3 * | ***************************************************************************************** [Mapping the Hamming Distances of every possible pair of codes in a set of eight 6-bit codes. Distances between matching codes are left blank.] From this table, we can see that each pair of codes has a Hamming Distance of either **3** or **4**. The number of errors that can be corrected is limited to the smallest distance between any pair of codes (in this case, **3**.) We can now use the formula above and substitute \(d\) with _3_, showing that we can correct one error with this set of codes: \begin{equation} \Big\lfloor \frac{(3 - 1)}{2} \Big\rfloor = 1 \end{equation} The formal term for a set of codes that have a maximum distance between all pairs of codes is **Maximum Distance Separable Codes** or, more commonly, **MDS Codes**. The size of each code depends on the number of data bits they are intended to represent plus the number of additional bits that are needed to provide error detection and correction features. For example if a data word is 6 bits, then adding an additional 4 bits (often called _parity bits_) would allow for a single bit of error correction. In common parlance, this would be _a 10-bit code with 6 bits of data_. !!! Note: A Note About Notation A common notation for describing MDS codes takes the form: \[(n, k, d)\] where \(n\) is the total number of bits in each code, \(k\) is the number of bits of data represented by each code, and \(d\) is the minimum distance of the code set. This notation is often shortened by omitting the \(d\) component: \[(n, k)\] It may also be helpful to note that the number of parity bits in the code is \(n-k\). Also, an MDS code set will contain \(2^k\) codes. ## MDS Code Generation MDS codes are generated using the __mdscodes__ tool (see the Generating Codes with mdscodes section.) For those interested, this section will cover the process by which this tool generates codes as well as some ways in which it deviates from standard implementations to provide for the specific requirements related to scanning codes printed on decks of cards. MDS code generation does not require a complex code solution. A naive approach could simply perform an exhaustive search through the code space and reporting the largest minimum distance of all combinations of codes sets. Of course, this approach does not scale well as the number of bits in a code increases. There are a number of different analytic approaches for generating MDS codes efficiently. The following sections will cover the solutions used in this software. ### Generator Matrix The most common analytic approach for generating sets of MDS codes is to use a generator matrix. The dimensions of a generator matrix would be a \((n \times k)\) for a \((n, k)\) code set. There are also many approaches for creating generator matrices. The approach used here makes use of a binary value containing \(n-k+1\) bits, where the MSB & LSB is always **1**. The matrix is created by shifting this value into a different position within each row of the matrix. In the final matrix this produces a diagonal pattern that is clearly recognizable. This binary value is referred to as a _Generator Polynomial_. \begin{equation} \begin{pmatrix} 1&0&0&1&1&0&0&0&0&0 \\ 0&1&0&0&1&1&0&0&0&0 \\ 0&0&1&0&0&1&1&0&0&0 \\ 0&0&0&1&0&0&1&1&0&0 \\ 0&0&0&0&1&0&0&1&1&0 \\ 0&0&0&0&0&1&0&0&1&1 \end{pmatrix} \end{equation} _A **(10 x 6)** Polynomial Generator Matrix using the polynomial **10011**. The value starts with the MSB of the polynomial value aligned in the left-most column of the matrix and with each successive row, the polynomial is shifted to the right by one bit._ To generate a set of codes from this matrix, each 6-bit data value is treated as a 6-dimensional vector for each of the \(2 ^ 6 = 64\) data values. \begin{equation} \begin{pmatrix} 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \end{pmatrix} \begin{pmatrix} 1&0&0&1&1&0&0&0&0&0 \\ 0&1&0&0&1&1&0&0&0&0 \\ 0&0&1&0&0&1&1&0&0&0 \\ 0&0&0&1&0&0&1&1&0&0 \\ 0&0&0&0&1&0&0&1&1&0 \\ 0&0&0&0&0&1&0&0&1&1 \end{pmatrix} = \begin{pmatrix} 0&1&1&0&0&0&1&1&1&0 \end{pmatrix} \end{equation} _A 6-bit data value of **011010** treated as a 6-dimensional vector and multiplied by the Polynomial Generator Matrix from above, producing the 10-bit code **0110001110**._ Not every polynomial value will create a Generator Matrix capable of producing the optimal set of MDS codes. A brute-force search is used to find the polynomial that produces the optimal set of MDS codes. This does not scale well. However, given that the largest anticipated code set is roughly \((18, 6)\) the resulting polynomial is 13 bits, describing a search space of 8,192 possible values. Moreover, as the LSB and MSB of the polynomial are always **1**, they can be removed from the search space cutting the number of iterations by 75% to 2048 polynomials. !!! Note: Further Reading Dr. Richard Tervo from the University of New Brunswick has provided an interactive tool for generating Polynomial Generator Matrices for use in MDS code generation. This tool can be found at [http://www.ee.unb.ca/cgi-bin/tervo/polygen2.pl](http://www.ee.unb.ca/cgi-bin/tervo/polygen2.pl). ### Reversible & Palindrome Codes Some use cases may require the use of cards that are face-up in the deck. When this happens, the bits of the code will appear in reverse order. This is problematic for MDS code sets as a reversed code may exactly match another code, or possibly error correct to yet a different code. To avoid these issues, the scanner does not attempt to read codes in both directions. Instead, codes that can be read in forward- or reversed- bit order are generated either as _Reversible Codes_ or _Binary Palindromes_. The difference between _Reversible_ and _Palindrome_ codes is in their ability to detect when the code is reversed. A _Palindrome_ code reads as the same code in both directions. Because of this, its directionality cannot be determined. That is to say, of a card is face-up in the deck it will be read as a normal card. In contrast, a _Reversible_ code does provide directionality when being read in each direction. This allows the software to determine the card and if the card is face-up in the deck. _Reversible_ codes use a special set of codes in which each code represents two valid MDS codes: one read in the forward direction and one in reverse. Both, _Palindrome_ and _Reversible_ codes are \(2k + 1\) bits wide, a minimum distance of 3, and 1 bit of error correction. ### Custom Enhancements The scanning process can be aided by manipulating the codes that are used to mark the edges of cards in a deck. These manipulations are not required but they have proven to produce slightly better scanning results. First, any code that is all 0s or all 1s can place a small burden on the scanner's ability to decode the deck of cards. To avoid this, every code is XORed with a mask containing an alternating bit pattern. This doesn't alter the minimum distance between the codes as every code has been manipulated in the same way. Note that for _Palindrome_ codes, special care is taken to ensure the mask is also a palindrome in order to preserve the reversibility of the final set of codes. Second, a process called binary distribution optimization is run on the full code set in which every code is XORed with a mask intended to provide as even a distribution of bits throughout the code as possible. This rearrangement of bits reduces the likelihood of a stacked deck of cards having large areas of all 0s or all 1s. This helps the process of gathering Mark Lines (see the Gather Mark Lines section) as an even bit distribution improves the results of the moving average used for determining if a pixel in the image is from a printed mark or an empty mark. As this process would affect the reversibility of _Reversible_ and _Palindrome_ codes, this option is only available for codes generated from a generator matrix. Finally, some codes can produce a recognizable pattern when stacked sequentially (as would be the case of a deck stacked in New Deck Order.) As many magic tricks make use of New Deck Order, these patterns can stand out and make it easier for the marks to be noticed when printed on a deck, even with IR and UV inks. To reduce the probability of these visible patterns, the codes are shuffled in a pseudo-random fashion. ![A palindrome code set, before (left) and after (right) shuffling. Although there is still some amount of recognizable pattern in the shuffled set, the visible pattern is largely reduced.](img/shuffle.png) ## Correcting Errors Errors in scanned values that haven't exceeded the maximum number of correctable bits can be error corrected to a valid code. This is done by finding the closest (via Hamming Distance) valid code to the scanned value. Readers familiar with traditional approaches to error correction might expect to read about _parity check matrices_ and _syndrome vectors_. However, as described in the MDS Code Generation section this software doesn't always employ the use of a generator matrix. The approach used here leverages the specific requirements of this software to provide a more efficient solution while providing improved error correction rates. A naive approach for correcting errors in codes as they're scanned would calculate the distance between the scanned value and each valid code, storing the single valid code with the smallest distance. In the case where the scanned value was correct the smallest distance would be **0**. If the scanned value had too many errors, then the smallest distance might match more than one valid code, in which case it would be possible to determine (but not correct) an error. A scanned value with too many errors might also match a single incorrect code, in which case the resulting code would be undetectably incorrect. Given that this software uses relatively small codes (generally fewer than 18 bits) we can simplify this process with a lookup table that represents the full code space with each possible code mapped to the error-corrected code (or a value designated for uncorrectable errors.) For a common 13-bit code this table would contain 8,192 entries. In practical terms of this software, a code scanned from the edge of a card is used as an index into such an error correction table. The value from the table will either result in the valid (possibly error-corrected) code for a specific card in the deck or a designated value that represents an uncorrectable error. ### Improving Error Correction Results The error correction table mentioned above is populated in a series of iterative steps, with each iteration populating table entries with increasing error correction bit counts. If an entry in the table has an undetermined error correction result, the table entry is marked as uncorrectable. This happens when there is a _collision_ in which a single code could error-correct to two different codewords. These uncorrectable entries result in unused space, or _collisions_, in the table. ******************************************************************** * ░░░█░██░░░░█░██░░██░░░░█░██░░░░█░█░░█░░█░█░░█░░██░░█░█░░█░░█░█░░ * * ░██░█░░░░██░█░░░█░░░░██░█░░░░██░█░░█░░█░█░░█░░█░░░█░█░░█░░█░█░░█ * ******************************************************************** [An error correction map for a small \((7,3)\) code set. Solid blocks denote table entries containing codes (either exact or error-corrected) while hashed blocks represent collisions. This map contains \((2^7=128)\) entries in which 80 are collisions (62.5%).] The number of cards in a deck doesn't usually land on a power-of-two boundary. Representing 52 cards requires 6 bits of data but not all of the \(2^6=64\) values are used. These unused values create slack in the error correction table that can provide additional error correction. The map above was generated using the full set of \(2^k=8\) (where \(k=3\)) codes. By reducing the total set of codes from 8 to 5, we find that the slack creates opportunities in the table for greater levels of error correction with up to as many as 3 bits of error for some codes. ******************************************************************** * ███████████░█████░░████░█░█████░█░██░██░████████░██░███████░████ * * █████████░░█████░████░░█░█████░█░██░██░███████████░████░██░████░ * ******************************************************************** [The same error correction map as above, but with only 5 of the 8 possible codes in use. Note that much more of the table has been populated with error correcting codes. This map contains 26 collision entries (20.3%).] The map above shows a considerably greater level of error correction than traditional methods. In practical use cases of code sets used for scanning 54-card decks, the use of error correction tables leveraging unused codes enjoys varying degrees of improvement. Measured in terms of an increase of the number of codes that can be error corrected, scatter tests show improved error correction rates that range from as low as 3% to greater than 25% depending on the code type. ## Generating Codes with mdscodes _mdscodes_ is a command-line tool that generates error correction codes specifically designed for marking the edges of cards. These codes represent the contents of the **cardCodesNdo** array that is part of each deck definition found in the _decks.json_ file (see The Fields of a Deck Definition section.) !!! Note: Before generating a set of codes There may already be a deck definition that meets your specific needs in the _decks.json_ file. If so, it is recommended to use existing definitions rather than creating a new one. The specifics of _mdscodes'_ command line options may change over time, so please consult _mdscodes_ for proper usage with the command: ~~~~~~ mdscodes help ~~~~~~ !!! Note For a deeper understanding of the options (such as _shuffling_ and _binary optimization_) consult the Custom Enhancements section. For most cases, these options should not be needed as they are enabled by default since they provide moderate improvements to scanned results. When generating matrix-based codes where the code size can be specified, it is important to select the appropriate number of bits. Larger code sizes do not always result in higher error correction rates. Code bits | Min dist | Correctable bits | EC Rate :---------:|:--------:|:----------------:|:------------: 10 | 3 | 1 | 59.8% | | | 11 | 4 | 1 | 33.0% 12 | 4 | 1 | 32.0% 13 | 4 | 1 | 31.8% | | | 14 | 5 | 2 | 61.0% | | | 15 | 6 | 2 | 38.2% 16 | 6 | 2 | 36.3% | | | 17 | 7 | 3 | 64.2% | | | 18 | 8 | 3 | 39.7% [A table of error correction rates for codes representing 6 data bits. The **EC Rate** represents the percentage of correctable values in the full code space. EC Rates are calculated from error correction tables generated from a subset of 54 values.] The table above is separated into groups based on the minimum distance for each code set. Notice that within each group, the EC Rate is the highest for the first entry in each group. For example, an 11-bit code provides a higher EC rate than a 13-bit code. Also important is that codes with an odd numbered minimum distance provide better EC Rates than codes with an even numbered minimum distance. Finally, it is important to consider the risk of scanning errors increases as the number of code bits increases. For non-matrix-based codes, the number of code bits is not selectable. These code sets have lower error correction rates than matrix-based code sets, but offer features that are not available with matrix-based codes. Code bits | Min dist | Correctable bits | EC Rate :--------------:|:--------:|:----------------:|:------------: 13 (palindrome)| 3 | 1 | 17.0% 13 (reversible)| 3 | 1 | 17.0% [A table of error correction rates for palindrome and reversible codes representing 6 data bits. The **EC Rate** represents the percentage of correctable values in the full code space. EC Rates are calculated from error correction tables generated from a subset of 54 values.] # Marking ![A photo of the workstation taken during the discovery phase of applying the first marks using IR absorbing ink. This process used an early prototype of a 3D-printed stamping rig that was abandoned for a much simpler, more flexible and inexpensive rig. Various chemical solutions were tested for mixing inks as were various daubers for evenly applying the ink to the stamp. Also visible along the right is a breadboard for testing various IR LEDs for use with the ink.](img/marking-r&d.jpg) This section will cover two different approaches to applying marks to the edges of individual cards. The first is a manual marking technique that uses a Medium Sharpie marker. This requires patience and a steady hand, and probably a few spare decks. This method is only recommended for marking decks with black ink. In general, expect to spend up to 3 hours on a single deck. The second technique uses a custom printed stamp. This provides superior results and can be used with any type of ink. With a bit of practice, a deck can be marked in about 10-15 minutes. It is important that the marks have these traits: * **Landmarks are clean and sharp** - Clean and sharp landmarks will make it easier for the edge detection used to locate the deck in the video frame. Furthermore, the innermost landmarks are used to locate the rows of bits on each card. If these landmarks are messy, then the scanning process will have a difficult time scanning the deck. * **Landmarks are consistent across all cards** - The process of tracing the deck uses an algorithm that follows the contour of the innermost landmarks. This algorithm relies on the luminosity of the landmark being fairly consistent across the entire deck. If the landmarks have inconsistent luminosity from card to card, the scanning process will often fail. * **The marks must be properly centered** - Cards can be rotated (end-for-end) or flipped (face-up) in the deck. In order for the landmarks to line up properly, the entire code must be perfectly centered. Also note that the more bits there are in your code, the less room there is for error when centering the marks within the deck. ## Manually Marking A Deck ![An early prototype deck using the manual marking technique.](img/manual-marks.jpg) Manually marking a deck involves using a straight edge and a Medium Sharpie marker. For the landmarks, this is a fairly straight-forward task as the landmarks are applied to the entire deck. Marking the _Bit Marks_ requires an additional step of collecting the cards that have a specific bit set and applying the marks to them as a group and repeating this process for each Bit Mark. !!! Note: Before You Begin * Have a few Medium Sharpie markers handy. * Use a new sharpie. Experience has shown that a Medium Sharpie is only good for a couple decks before it should be replaced. * Be sure to have a few new decks of cards handy. Mistakes are likely to happen and spare cards are especially handy for templates and other uses. * Always mark a new deck and take care to keep the cards in perfect condition. * You will need access to the _CardBars_ application. What follows should be thought of as a rough guide and should not be considered authoritative. There is a lot of room for improvement. Put on your Maker hat and be creative. ### Generating A Mark Map The first step in manually marking a deck is to generate a _Mark Map_. A Mark Map provides a list of cards that will need to be marked for each Bit Mark in a deck. To generate a Mark Map, open the tool _CardBars_ and select the appropriate code from the **Codes** menu. Once a code is displayed in the application, select **Image->Dump mark map**. The Mark Map will be written to the log (usually in **/tmp/whisper.log**). If running from Xcode, the Mark Map will appear in the Output view. ************************************************************************** *Bit: 00: AH 2H 3H 4H -- -- -- -- -- -- -- QH -- AC -- 3C 4C -- -- -- ...* *Bit: 01: -- -- 3H 4H 5H 6H 7H -- -- TH -- QH -- -- -- 3C -- -- -- 7C ...* *Bit: 02: AH -- -- -- 5H -- -- 8H -- -- JH QH KH -- 2C 3C -- -- -- 7C ...* *Bit: 03: -- 2H 3H 4H -- -- -- -- 9H TH -- -- KH AC -- -- -- 5C 6C 7C ...* *Bit: 04: -- -- 3H -- -- -- 7H -- 9H -- JH QH -- AC -- -- -- 5C -- 7C ...* *Bit: 05: -- -- -- -- -- 6H -- 8H -- -- -- QH -- -- -- 3C -- 5C 6C -- ...* *Bit: 06: AH -- -- 4H -- 6H -- 8H 9H TH -- QH KH AC 2C -- -- 5C -- 7C ...* *Bit: 07: AH -- -- -- -- 6H -- 8H 9H TH -- -- KH -- -- -- 4C -- -- 7C ...* *Bit: 08: -- 2H -- -- -- -- 7H -- -- TH JH -- KH AC 2C -- 4C 5C 6C -- ...* *Bit: 09: AH -- -- 4H 5H 6H -- -- -- -- JH QH KH AC -- -- 4C -- 6C 7C ...* *Bit: 10: -- -- -- 4H 5H -- 7H -- 9H TH JH -- KH AC -- 3C 4C 5C -- 7C ...* *Bit: 11: AH 2H 3H 4H -- -- 7H 8H -- -- -- -- KH AC -- -- -- 5C 6C 7C ...* *Bit: 12: AH -- -- 4H -- 6H 7H -- 9H TH -- -- -- AC 2C 3C 4C -- 6C -- ...* *Bit: 13: AH -- 3H -- -- -- -- 8H -- TH JH QH -- AC -- -- -- 5C -- 7C ...* ************************************************************************** [A section of a **Mark Map** for a 14-bit code, showing only the first 20 cards for each bit. Each row provides a list of cards that will require the bit to be marked.] ### Creating A Pair Of Templates The next step is to create a pair of templates that can be used as a guide for mark placement. CardBars can be used to generate a properly scaled printable image of the full code (**Image->Save to desktop**.) The image will scaled using the physical dimensions from the Deck Definition so it is important that the scale not be altered when printing. It may be helpful to fill in alternating columns of bits in the printed mark with a colored marker. Be sure to use a straight edge and be as precise as possible. This provides a consistent guide to mark locations in areas where the template contains no printed marks visible when wrapped around the template cards. To create a template, start by gathering 5 spare cards and taping them together into a small stack. Next, cut out a section of the printed mark and wrap it over the end (or side, if you intend to mark the sides) of the stack of cards. Center the template carefully before taping it into place. Two templates will be needed, one on each side of the deck. Proper alignment can be tested by holding the templates together to ensure that the marks line up properly. ### Applying The Marks To The Deck ![An early prototype deck using the manual marking technique. The templates are visible above and below the deck, and a spare card is used as a straight edge. This picture was taken just before a column of bits were to be applied to a subset of cards from the deck.](img/manual-process.jpg) Start by stacking the entire deck between the templates and carefully holding them tightly together in a way that doesn't bend or flex the cards. The cards in the deck should always be facing you. The goal is to create a tight stack of cards sandwiched between the templates that won't move when applying marks. Start by marking the landmarks with the Sharpie. Use a spare card used as a straight edge. It will likely take a few passes in each direction with the marker to ensure the mark is dark. Slide the straight edge over a little and continue marking until the mark is the proper width. If the deck is to be marked on both ends remove the deck from the templates, rotate it 180 degrees and repeat the marking process. Be sure that the cards are still facing you after rotation. Marking the Bit Marks on the deck follows much the same process as the landmarks. Use the Mark Map to collect the subset of cards needed the first Bit Mark and mark just those cards. Repeat the process for the next Bit Mark until all Bit Marks have been applied to the deck. !!! Note: Bit Ordering The bits in the Mark Map are in order from left-to-right. That is, when the deck is stacked face-down, bit 0 from the Mark Map will be the left-most bit on the deck. After completing the full set of bits, the deck will be fully marked. Stack the deck and examine it. Compare it with the quality of the marks in the image at the top of this section. If your marks are of a similar quality, the deck should scan and read. Refer to the Examining The Quality Of A Deck section for more information on determining the quality of your marks. ## Stamping A Deck The following is an outline of the general process for applying Black ink to a deck of cards using a custom printed rubber stamp. It is strongly recommended to start with Black ink as a way to get familiar with the process before moving on to IR absorbing or UV reactive inks. The IR absorbing Inks section and the UV reactive Inks section will cover the details of obtaining and using these inks. ![A stamped deck. Stamped decks produce significantly higher quality marks with less effort.](img/stamped-deck.jpg) ### Obtaining A Stamp Stamping a deck requires a custom made rubber stamp and a simple stamping rig. Rubber stamps produce a significantly higher quality mark and can be used with all inks including IR absorbing and UV reactive inks. Stamps used during the development of this software were ordered from [rubberstamps.net](https://rubberstamps.net). The stamps were always high quality and the service was very good. The specific stamps used during development were _Unmounted Stamps_ from the _Hobby_ section of the website. Large stamps work best so the stamps recommended here are the [8" x 10" Sheet of Unmounted Rubber](https://www.rubberstamps.net/ProductDetail.aspx?ProductID=UNMOUNTED16) stamps. These rubber sheets can provide up to 3 codes each. The first step is to use _CardBars_ to generate the stamp image for the code (or codes) used in the order. Launch CardBars, select the appropriate code from the **Codes** menu, then use **Image->Toggle rubber stamp** to produce an elongated stamp image. Finally, use **Image->Save to desktop** to save the stamp image. The stamp images produced by CardBars will match the physical scale of the codes as defined in their Deck Definition. The stamp image will be 600dpi, the same resolution used by [rubberstamps.net](https://rubberstamps.net). ![A rubber stamp image produced by CardBars.](img/mds18-54-rubberstamp.png width="10%") The stamp image produced by CardBars can be directly used when ordering a rubber stamp, but it is more cost effective to combine multiple stamps onto a single 8" x 10" sheet. When doing so, be careful not to alter the dimensions or DPI of the images. Stamps used during development were typically printed in groups of three. These stamps also included a few custom modifications made to the final combined image. These modifications include: 1. Separating the landmarks from the Bit Marks 2. A small centering line above and below each code 3. A text label above each code ![**LEFT**: An image used to order a stamp with three codes on a single 8" x 10" rubber stamp sheet with custom modifications. Notice the text label is reversed so it is readable on the final stamp. **RIGHT**: The final 8" x 10" rubber stamp that was created from the image.](img/stamp-generation.png) !!! Note: Separate Landmarks Separating the landmarks in the stamp image is an important step if the stamp is intended to be used for IR absorbing inks. These inks are fickle and can be difficult to work with. Separating the landmarks allows the landmarks to be stamped all at the same time, largely mitigating the greatest challenge in working with these inks. ### Building A Stamp Rig A stamp rig is simply a flat surface with a guide rail along one side. The material surfaces should not absorb moisture and allow for easy cleaning. Metals, coated or laminated materials work best. The guide rail should not have sharp edges and should be about 3/8" (1CM) high. The stamp rig used during development was inexpensive, simple to build, and worked very well. It was built from the following items: * White Laminated Wood Shelf (12" x 24") by Rubbermaid [[Link](https://www.homedepot.com/p/Rubbermaid-White-Laminated-Wood-Shelf-12-in-D-x-24-in-L-FG4B7900WHT/100679070)] * 24 in. White Single Track Upright for Wire Shelving by Rubbermaid [[Link](https://www.homedepot.com/p/Rubbermaid-24-in-White-Single-Track-Upright-for-Wire-Shelving-FG4A6701WHT/100006607)] * Half-inch wood screws (quantity 3) ![The stamp rig used during development pictured with a mounted 10" stamp and card alignment markers, a bottle of IR absorbing ink, an ink reservoir and foam dauber, and a paper towel for blotting.](img/stamp-rig.jpg width="50%") Simply attach the guide rail along one side of the rig with screws. Be sure your screws are shorter than the depth of the board. ### Mounting The Stamp To The Stamping Rig If the stamp sheet contains multiple codes, start by separating those codes with a straight edge and a razor blade. Centering the stamp on the rig is crucial. It must be as precise as possible, within about 0.2MM. This was achieved with the use of centering marks printed directly into the stamp and a centering card. Create a centering card from a spare card. Carefully draw a thin centering line with a fine ball-point pen running through the center of the edges to be marked. For example, if the narrow ends of the card are to be marked, the centering line should be drawn from the top of the card to the bottom, through the exact center of the card. Place the stamp on the rig roughly where it belongs. Adjust the top of the stamp by holding the centering card against the guide rail above the centering line at the top of the stamp. Ensure they are perfectly aligned. Repeat this process at the bottom of the stamp. Because the stamp is made of rubber, be careful to adjust the entire stamp when shifting positions so that the entire stamp is centered and not just the top/bottom sections. Continue centering the stamp at the top and bottom until you are satisfied that the entire stamp is properly centered. !!! Note: Verifying Center Once you have the stamp centered in place, turn the centering card around to face the other direction and ensure that the centering marks on the card are still perfectly aligned with the centering marks on the stamp. If the marks don't line up, this means that the marks on the centering card are not exactly centered. Tape the stamp into place. The stamp has a slightly sticky backing, so it shouldn't require much adhesive to keep it from moving around. ### Card Alignment Markers Card alignment markers provide a means to locate the row of Bit Marks for a given card. The Bit Marks on the stamp are printed from top-to-bottom in New Deck Order, so the order of the Card Alignment Markers should follow **faceCodesNdo** (as defined in the The Fields of a Deck Definition section.) These should be printed on a sheet of paper with spacing that properly matches the spacing of the rows of Bit Marks on the stamp. The narrow column of card alignment markers should be cut out of the printed page and taped next to the Bit Marks, directly onto the stamp. See the image at the top of the Building A Stamp Rig section for an example. ### Stamping Individual Cards !!! Note: Before You Begin * You will need: - A Black ink stamp pad - A bottle of stamp cleaner - A set of sponge daubers of various sizes [[example](https://www.amazon.com/Sponges-Sponge-Brushes-Painting-Acrylic/dp/B0BNL2D6R2/ref=sr_1_9?keywords=sponge+daubers&qid=1687394789&sr=8-9)] - A few new decks of cards * Always stamp a new deck and take care to keep the cards in perfect condition throughout the process. Prepare a new deck of cards in order of the card alignment markers. The top card should match the first card alignment marker and the bottom card should match the last card alignment marker. Set the deck of cards aside, face down. Apply the ink to the dauber by pressing it into the stamp pad. Be sure the dauber is fully coated but not saturated. Apply a thin coat of ink to every raised mark on the stamp using the dauber. Some ink will likely get applied to the valleys in the stamp - this is fine as long as the ink isn't allowed to pool in those valleys. The color of the stamp should not show through the ink on the raised surfaces of the stamp. It is time to begin marking cards. Take the top card from the stack and while holding it against the guard rail, align it with the top row in the stamp. The card should be facing the bottom of the stamp. That is, if the top of the stamp is farthest from you, then the card should be facing you. In a quick motion, press the card firmly down onto its row in the stamp then lift it off the stamp. Be careful not to press so firmly that the card bends. The card should be in contact with the stamp for no longer than 1/2 second. This quick application helps to control the amount of bleed. Repeat this process for a total of 5 applications. Each time, slightly adjust the position of the card within its row on the stamp. With a bit of practice, a card can be pressed onto the stamp 5 times over a period of about 2 seconds. If the deck is to be marked on opposite sides, rotate the card 180 degrees (still facing you) and repeat the process. Set the card aside, face-up, and grab the next card from the deck. Continue this process, stamping cards from the original deck and placing them onto the face-up stack. (###) Stamping Landmarks If your stamp has separated landmarks, allow the ink to dry on the deck for a few minutes before stamping the landmarks. Place 5 spare cards on the top of the deck and 5 spare cards on the bottom of the deck. These additional cards will help control the ink's bleed. Carefully stack the entire deck (including the additional cards) into a perfectly squared stack. Hold the deck firmly with two hands above the landmark section of the stamp, against the guard rail. The cards in the deck should face you. One hand should hold the deck at the top, ready to press the deck down onto the stamp. The other hand should hold the deck near the bottom to keep the cards tightly together where the deck will contact the stamp. Being sure to keep the deck against the guard rail, slowly press the full deck onto the stamp and hold it there firmly. While holding the deck down, slowly rock the deck forward and back a few times with your top hand, allowing the deck to bevel slightly. This action allows the cards to be marked thoroughly in a single stamp action. The deck should be in contact with the stamp for 3-5 seconds before lifting it from the stamp. If the deck is to be marked on opposite sides, be sure to reapply ink to the stamp before repeating this process for the other side. Remove the spare cards from the top and bottom of the deck and visually inspect the quality of your marks. See the Examining The Quality Of A Deck section for a thorough examination. For cards that are found to be problematic, try re-stamping the problematic cards. If the deck is intended to be used for testing, problematic cards can be swapped from other decks and stamped. Do not swap cards if the deck is intended for use in a performance. Every deck has a slightly different cut than its siblings. !!! Note: Cleaning Up Always clean your stamp with stamp cleaner before storing it away. ## UV Reactive Inks ![A deck marked with a UV reactive ink.](img/uv-ink.jpg) UV reactive inks are generally clear liquids that are almost entirely invisible when applied to the edges of cards. When a UV light is shined on these inks, they glow (fluoresce) in a variety of colors. If you've ever had a stamp on the back of your hand using an ink that shines under a black light, you've encountered this type of ink. The UV Ink tested during development was _Opticz All Purpose Invisible Blue UV Reactive Ink_. [[link](https://www.amazon.com/Opticz-Purpose-Invisible-Blacklight-Reactive/dp/B00GP9ORB8?ref_=ast_sto_dp)]. The UV LEDs used during testing were found [[here](https://www.amazon.com/Dazzling-Toys-Invisible-Marker-Stuffer/dp/B00N40MNFI/ref=sr_1_3?dchild=1&keywords=uv+invisible+ink&qid=1606247005&s=home-garden&sr=1-3)]. Note: these LEDs are not very good quality, but sufficed for the limited testing that was done with UV inks. !!! Note: How UV Reactive Inks Work Ultraviolet (UV) can be thought of as a form of light that is higher frequency than visible light, just outside the range of the human eye's ability to see. UV reactive inks contain a chemical that converts high frequency energy (Ultraviolet) into a lower frequency energy (visible light) making them glow. This process is called down-conversion. (###) Advantages * Inexpensive and readily available * Almost entirely invisible * With a slight modification, easily used with a stamp to apply to cards * No special camera is needed in order to capture and decode a deck * Decks last a very long time (###) Disadvantages * UV light should be used with caution * The UV LED and ink glow visibly and can be seen by spectators without preventative measures ### Use With Stamping These UV inks use an Isopropyl Alcohol solvent. This solvent dries very quickly making this ink difficult to use with a stamp. To mitigate this, vegetable glycerin was added to the ink in a ratio of 6 parts ink to 1 part vegetable glycerin. The vegetable glycerin used was Aura Cacia [[Link](https://www.auracacia.com/aura-cacia-organic-vegetable-glycerin-4-fl-oz/)]. This ink+glycerin mixture can be used in the process described in the Stamping Individual Cards section with the following modifications: * Since this ink is clear, it's difficult to judge proper application to the stamp. This can be mitigated with a lamp or portable work light positioned in a way that allows you to see the light reflected off the stamp. Use the light reflection when applying the ink to the stamp to ensure full coverage. * There will be no ink pad. Use a small shallow dish as an ink reservoir. Place a few drops into the reservoir. Treat the reservoir as you would an ink pad, replenishing the blotter as necessary. * A little ink goes a long way - a thin coat on the stamp is all that is needed. It is important that the ink coat only the top of the stamp. If the ink seeps into the valleys between marks on the stamp, this excess ink will act as a reservoir and will be soaked up by the fibrous edge of the card, causing excessive bleeding. ## IR Absorbing Inks !!! Note: Author's Note I will cover it in as much detail as I can remember (it's been a few years). Please forgive me if you find this section a bit pedantic. To me, these details are important. This was my process. You will likely make your own alterations that work best for you. You may even -- and I hope you do! -- find a better way altogether. If you do, please share it with the community. A final note before we begin - you may find it helpful to re-read this section after your first few attempts. You may, after all, find a new appreciation for the excruciating detail. :) ![A deck marked with an IR absorbing ink. This image was captured under IR lighting with a Raspberry PI NoIR camera and an appropriate IR filter.](img/deck_under_ir.jpg) IR absorbing inks are generally Yellow or Green liquids that dry almost clear making them virtually invisible, even when being examined by a trained professional. !!! Note: How IR Absorbing Inks Work IR inks work by reflecting most of the light in the visible portion of the electromagnetic spectrum, while absorbing light in the IR portion of the spectrum. There are various types of IR absorbing inks, each with different properties. Some inks are specifically formulated to focus their absorption to a narrow band of light in the IR portion of the spectrum. This makes them almost invisible to human eyes, while appearing very dark under proper IR viewing conditions. Two inks were used during testing: * NIR 850nm visible absorbing dye - Manufactured by Qingdao Topwell Chemical Materials Co., Ltd. - Purchased through [Alibaba.com](https://topwellchem.en.alibaba.com/product/62078268165-805014998/NIR_850nm_visible_absorbing_dyes_for_security_application.html?spm=a2700.icbuShop.41413.9.461b6f25V3Lgcc). - Cost: 20g for $160 (in March, 2019). 20g is way more than I ever needed. 1g would have sufficed. * DT3-88A - Manufactured by [Epolin](https://www.epolin.com) - Purchased directly from the manufacturer - Cost: $65 for 1g Both of these inks worked well with different properties. The Epolin ink was preferred as it tended to be less visible, but had a slightly shorter shelf-life once marked on the deck. These inks absorb light in a narrow band of the IR portion of the spectrum centered on about 850nm. If you were to use a wide spectrum IR LED without any IR filtering, the marks would be very difficult to see since the ink would only absorb a small portion of the light visible to the IR camera. To resolve this, we combine the use of an IR light source and filter that are also tuned to this same narrow band of the spectrum. In this way, the only light reaching the camera is from that narrow band. The LED and filter used during testing: * LED - Lite-On LTE-R38386A-ZF-U [[DigiKey](https://www.digikey.com/en/products/detail/liteon/LTE-R38386A-ZF-U/6819917)] [[Datasheet](https://us.liteon.com/upload/media/news/20161228%20LTE-R38386A-ZF-U%20DATA%20SHEET.pdf)] - Cost: $1.79 each - Notes: While this LED is a surface mount component, it is very bright with a 150-degree angle. Using standard through-hole components tends to produce narrow beams of light that may not illuminate the entire deck and certainly won't illuminate it evenly. * Two filters were used during testing - Optolong LP800nm (long pass filter) and BP850nm (band pass filter.) - Both purchased from Optolong [[Link](https://www.optolong.com/)] through Alibaba. - Cost: These were custom made. Some were 10mm diameter and some were 5mm diameter. Expect to spend a few hundred USD on filters. - Notes: The band pass filter is preferred as it filters out all light except the specified portion of the spectrum. The long-pass filter on the other hand only filters out light frequencies below the specified limit. Handle with care. These are glass filters and break easily. (###) Advantages * With proper application they are virtually invisible and can survive close inspection * Unlike UV inks, they remain invisible during the performance (they do not fluoresce when hit with IR light) * Can use a commonly available solvent (Isopropyl Alcohol - 91%) as a solvent (###) Disadvantages * More expensive than Black Ink or UV reactive ink * Very difficult to use with a stamp, requiring practice, patience (and a lot of practice decks) * Decks must be stored in air-tight, no-light environment * Ink degrades over time, becoming more visible to the human eye and less readable under IR conditions in just a few weeks * Requires special viewing conditions: - A camera lens that does not filter IR light - An IR filter - An IR LED !!! Note: Author's Note This author is not a chemist. A person familiar with the arcane art of alchemy may likely know of ways to mitigate some of the more challenging disadvantages (namely the evaporation rate and limited lifetime of marked decks.) While it's true that I found them difficult to work with, I also found it _very rewarding_ once the process has been dialed in with practice to produce a perfect deck. I did attempt to mitigate the evaporation rate by adding vegetable glycerin (similar to that discussed in the UV Reactive Inks section.) However, as these inks tend to dry clear, the use of vegetable glycerin resulted in marks that appear to never fully dry, remaining visible on the deck. ### Equipment Aside from the inks, you'll want to have these (or something similar) handy: * 8-Ounce Plastic Squeeze Bottles with Graduated Measurements [[link](https://www.amazon.com/gp/product/B075THYZ2M/ref=ppx_yo_dt_b_search_asin_title?ie=UTF8&psc=1)] * Stainless Steel Measuring Spoons [[link](https://www.amazon.com/gp/product/B00KH9PSNI/ref=ppx_yo_dt_b_search_asin_image?ie=UTF8&psc=1)] * 2 oz dropper bottles [[link](https://www.amazon.com/Bumobum-Essential-Tincture-Unbreakable-Measurements/dp/B0BB6MJDGQ/ref=sr_1_18?crid=28RO4AKAQJPZY&keywords=dropper+bottles+2+oz&qid=1687394397&refinements=p_n_feature_thirteen_browse-bin%3A34113015011&rnid=34112982011&s=industrial&sprefix=dropper+bottle%2Caps%2C134&sr=1-18)] * 1-inch sponge daubers [[link](https://www.amazon.com/Sponges-Sponge-Brushes-Painting-Acrylic/dp/B0BNL2D6R2/ref=sr_1_9?keywords=sponge+daubers&qid=1687394789&sr=8-9)] * Small dish used as an ink reservoir (similar to [[link](https://www.amazon.com/Colias-Wing-Multipurpose-Porcelain-Dishes-Set/dp/B07G9DSRS6/ref=sr_1_5?crid=1IZ2S00M3L35U&keywords=small+dish&qid=1687395399&sprefix=small+dish%2Caps%2C139&sr=8-5)]) * A work light with a large illumination surface area (similar to [[link](https://www.amazon.com/Coquimbo-Rechargeable-360°Rotate-Flashlight-Inspection/dp/B07G9X19G1/ref=sr_1_6?crid=OBARD1F0PXLE&keywords=work+light&qid=1687395630&sprefix=work+light%2Caps%2C118&sr=8-6)]) * Air and light blocking storage bags (similar to [[link](https://www.amazon.com/100-Pack-Mylar-Bags-Resealable/dp/B07ZJGLMRS/ref=sr_1_23?keywords=smell+proof+bags&qid=1687400227&sr=8-23)]) You will also need a fully functional IR rig handy, with the app running so you can see what the IR camera sees. You'll want to periodically inspect the deck as you go, so you can learn what works and what doesn't. ### Preparing The Ink The ink comes in the form of a powder (refer to the photo at the start of the Marking section, the ink is the rust colored powder in the pouch.) This ink needs to be mixed with IPA. The process below will create 8 oz of liquid ink. This is a lot of ink. You may only need 1 oz of ink, but a method for making smaller batches was never investigated. Here's how to prepare the ink: * Fill a squeeze bottle with 8 oz of 91% Isopropyl Alcohol. * Add a 1/32 tsp of ink powder (scrape the top of the spoon to level it.) Dip the spoon into the solution to get all the ink off the spoon. * Place the cap on the bottle tightly. While squeezing the bottle, listen to the cap for air leaks. Tighten the cap until you hear no air leak. * Shake vigorously for a minute or two. * Shine a flashlight sideways into the bottle and closely examine the solution. You should see small floating particulates. * Let sit for 2 hours. * Check the solution again with a flashlight to ensure there are no longer any floating particulates. * Your ink is ready. !!! Note: A note about ink longevity In powder form, the ink will last a very long time (years.) Once mixed into a solution, it is only good for about a week before it starts to degrade. Best results will come from freshly mixed ink. The ink degrades faster when exposed to UV light (sunlight) or open air. Store your ink in a dark place with the cap sealed tight. ### Use With Stamping ![One of these decks is marked with an IR absorbing ink, while the other is unmarked.](img/ink_comparison.jpg) You will be working with thin coats of ink on your stamp. These thin coats will evaporate very quickly (about 6 times faster than water.) From the time the ink touches the stamp, you will only have 5-10 seconds to work. Success requires preparation, efficiency and practice. Prepare your workspace with everything in easy reach. Your stamp rig should be directly in front of you with a comfortable reach to stamp cards. Just beyond the stamp rig should be a work light positioned such that the light reflects off of the liquid ink as it is applied to the stamp. On your dominant side (left/right) place the deck of cards to be marked. You will be pulling one card at a time from this deck and placing them directly onto the stamp. You may find it helpful to create a deck holder to make it easy to grab the next card. This author used a card box cut in half, angled up in the air with a stand made from an old card folded and taped to the box. !!! Note: Pay attention to the deck positioning It is easy to mark the deck in the wrong order or orientation. Make sure you understand the direction that each card should face while being marked. Also make sure you understand the order of the cards relative to the order of your stamp. Is the first card to be marked on the stamp row nearest you, or farthest from you? Practice a few cards to ensure that you don't need to think about it before you begin. On your non-dominant side, set aside an area to place marked cards. Take into consideration that you will be working quickly so you won't have time to square up the deck as it grows. You will also want to have your ink bottle near by, but keep your 2 oz dropper bottles, reservoir dish and sponge dauber closer. Squirt some of your ink into the 2 oz dropper bottle. Fill it about half way. Finally, you'll want your IR rig available on the one side with the app running so you can periodically place a card (or set of cards) in front of the camera to see the marks. Don't expect to get reads from short stacks (the software usually requires a minimum number of cards before it will attempt a read.) This author used a sheet of white paper with the camera at one end pointing along the paper. Placing a card on this paper with the edge facing the camera made it easy to see the quality of the marks during the marking process. At this point you should be ready to begin marking. ### Understanding The Ink On The Stamp During a performance, you'll want quick reliable deck reads. This requires clean marks, which requires the right amount of ink applied to each card. By extension, your primary focus will be on the amount of ink that is applied to the stamp. You will be using the dauber to apply the thinnest possible coat of ink on the stamp. The stamp should be damp, not wet. If you see the ink bulge (via surface tension) on the stamp, you have too much ink. If you see ink seeping into the valleys between the raised marks on the stamp, you have too much ink and likely have too much ink on the dauber or are pressing too hard with the dauber. There should also be even coverage across the row you are marking. You will find that at times, it will be necessary to pause marking to wait for the stamp to dry in order to re-apply the ink for proper coverage. All of this requires your ability to see the ink on the stamp clearly - use your work lamp positioned such that you see the reflection of the light in the ink. Since your ink will be applied in very thin coats, it will dry within seconds. Expect to mark one card at a time. Once your muscle memory starts to kick in, you'll get faster and can maybe get two cards at a time. Play around with it. You may find that you can apply a little extra ink to a row, grab a card, and wait for evaporation to reduce the ink to the right amount before dropping the card on the row. ### Applying The Landmarks Consistent landmarks are crucial for quick reliable reads. For this reason, your stamp should have the landmarks separated from the bit marks. This way, you can apply the landmarks to the entire deck at once. The process of applying the landmarks is the same as individual cards, except you will be pressing the entire deck onto the stamp instead of an individual card. ### Applying The Marks !!! Note: Required reading Before attempting this, be sure you have read the Stamping A Deck section for a good understanding of the overall approach to stamping individual cards. The process to mark a single card is: 1. Apply a small amount of ink into from the dropper into a small pool in the reservoir dish. About 5 drops onto the same spot is usually a good starting point. Note that if there is still ink in the reservoir, use fewer drops. Also, if you find that you're not getting enough ink (or too much ink) on the stamp, this is a good place to make an adjustment. 2. Soak up as much ink from the reservoir into the dauber as possible. 3. Tap the dauber onto the stamp row that you want to mark. Don't worry about ink on adjacent rows - it will dry. Use a light touch to ensure ink only sits on top of the marks and not in the valleys between marks. Do this with the work light positioned to allow you to clearly judge the amount of ink applied to the stamp. Note that as you progress through the stamp, you may need to adjust the position of your work light. 4. When you are comfortable with the amount of ink on the stamp, set the dauber aside and _quickly_ grab a card from your stack and place it on the row to mark it. Use the guide rail to ensure proper alignment. Tap the edge of the card onto the stamp a few times. This allows you to apply a bit more ink (for good dark marks) while reducing the risk of bleeding. 5. Place the marked card aside. 6. Repeat the process starting with #3. If the dauber does not have enough ink for good coverage, repeat step 1 and/or 2 as needed. Every 10 cards or so, place them in front of your IR camera to investigate the quality of the marks. You want marks that are: * Relatively dark (they won't be pure black) * Sharp, well defined edges (no bleeding) * Consistent (all marks across all cards are generally the same darkness) If your marks are too light, you can re-mark those cards. If your marks are bleeding, you're using too much ink. Throw the card away. If you are OK swapping that card with a card from another deck to replace it, feel free. ### Use And Care Of IR Marked Decks Storing your decks is important. If you leave your decks out on the kitchen counter (for example) you will probably find that they have faded and are difficult to read (if they read at all) the following day. You'll want to protect your decks from light and air. The equipment section includes a link to a set of storage bags that will work well for this, but any storage that keeps them from air and light will help them last as long as possible. You will find that even with this, your decks will read great for about a week and 'Okay' for perhaps the next week or two. Beyond that, the decks will likely not read well. ## Examining The Quality Of A Deck The quality of a deck can be visually examined using the _Abra_ client app. In Abra, open the hamburger menu and enable **Error Correction**. This is a debug visualization that highlights cards that required error correction during decoding phase. When using this feature, be sure that the deck is large in frame and is not moving. The error correction is updated each time a frame is received from the server so expect error correction updates to come at a high frequency, resulting in cards that appear to flicker Red. Some error correction is expected. Scanning data from live video is an inherently noisy process. Error correction plays an important role in mitigating this noise. ![Visualizing the use of error correction during deck scanning in real time. Cards tinted Red are those that required error correction in order to decode the deck.](img/error-correction-viz.png) (###) Interpreting the Error Correction Visualization * Cards randomly flicker Red throughout the deck. No card appears Red more often than any other card. No card stays Red for more than a frame or two. Only a few cards are Red at any given point. > This is the ideal scenario. > This deck is decoding very well. * A single card (or specific group of cards) tends to flicker Red more often than others. > These cards are having minor difficulty being decoded. Possibly a Bit Mark is too light and difficult to read. > If this deck was made from a stamp, try re-stamping the card. If that doesn't help (or > if it makes things worse), try swapping the card out with a freshly stamped card from > another matching deck. * A single card (or specific group of cards) tends to stay Red. > These cards are having real difficulty being decoded. Likely a Bit Mark has failed to mark > or a bit was marked incorrectly. > If this deck was made from a stamp, try re-stamping the card. If that doesn't help (or > if it makes things worse), try swapping the card out with a freshly stamped card from > another matching deck. * The deck refuses to decode > Verify that Abra is using the correct definition (selected across the top of the app) > that matches the newly marked deck. > > If this doesn't resolve the problem, try using the debugging visualizations to understand > where the deck is failing to read.